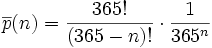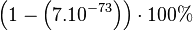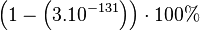Paradoxe des anniversaires - Définition

Introduction

Le paradoxe des anniversaires, dû à Richard von Mises, est à l'origine une estimation probabiliste du nombre de personnes que l'on doit réunir pour avoir une chance sur deux que deux personnes de ce groupe aient leur anniversaire le même jour de l'année. Il se trouve que ce nombre est 23, ce qui choque un peu l'intuition. À partir d'un groupe de 57 personnes, la probabilité est supérieure à 99 %.

Cependant, il ne s'agit pas d'un paradoxe dans le sens de contradiction logique ; c'est un paradoxe, dans le sens où c'est une vérité mathématique qui contredit l'intuition : la plupart des gens estiment que cette probabilité est très inférieure à 50 %.

(Par souci de simplicité, tout l'article est rédigé en supposant que toutes les années sont non-bissextiles. Prendre en compte le 29 février changerait peu les résultats, mais rendrait les calculs très délicats pour les applications où les personnes ne sont pas nées la même année)

Comprendre le problème

La clé consiste à se demander quelles sont les chances qu'aucune paire de personnes ne soit née le même jour. Pour chaque personne ajoutée dans la pièce, le nombre de dates non déjà prises diminue. La première personne a donc 365 choix, la deuxième 364, la troisième 363, la quatrième 362, et ainsi de suite.

Le problème consiste à se demander si une quelconque paire d'individus dans la pièce a la même date d'anniversaire.

Dans un groupe de vingt-trois personnes, il y a 23 x 22 ÷ 2 = 253 paires possibles, ce qui représente plus de la moitié du nombre de jours contenu dans une année. À partir de 28, le nombre de paires excède le nombre de jours, ce qui ne signifie évidemment pas qu'il est impossible de trouver un groupe de 28 personnes dont l'anniversaire est différent. En effet, le nombre de paires donne une intuition du problème mais n'explique pas la probabilité associée car cela reviendrait à additionner les probabilités d'évènements qui ne sont pas disjoints.

Démonstration

Nous donnons une preuve pour le cas d'origine, avec des jours d'anniversaires, mais cela se transpose simplement au cas de la généralisation énoncé.

Le plus simple pour obtenir le résultat annoncé est de calculer la probabilité que chaque personne ait un jour anniversaire différent de celui des autres. On va procéder par dénombrement, c'est-à-dire, que nous allons compter le nombre de cas où n personnes ont des jours d'anniversaires différents et nous diviserons par le nombre de possibilités. Il y a n personnes, pour chacune il y a 365 jours possibles, donc au total si on ne se fixe aucune contrainte, il a 365ⁿ possibilités. Si maintenant on veut des jours différents, nous obtenons un arrangement de n parmi 365, soit : .

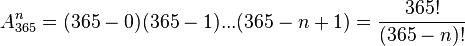
On a donc

Or, l'événement « un jour anniversaire différent par personne » est le complémentaire de « au moins deux identiques ». Par conséquent la probabilité recherchée est .

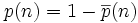
En faisant l'application numérique, on trouve 50,73 % pour vingt-trois personnes.

n	p(n)
5	2,71 %
10	11,69 %
15	25,29 %
20	41,14 %
25	56,87 %
30	70,63 %
40	89,12 %
50	97,04 %
60	99,41 %
80	99,99 %
100	99,99997 %
200	99,9999999999999999999999999998 %
300
350
>365	100 % (par le Principe des tiroirs)