Plan affine de Desargues - Définition
La liste des auteurs de cet article est disponible ici.
Bibliographie
- Emil Artin, Algèbre géométrique, Calmann-Lévy, traduction de Geometric algebra New York, Interscience Publishers, Inc., 1957, chap.II.
Structure d'espace affine
Espace affine (définition)
Un espace vectoriel sur un corps K (corps des scalaires) est un groupe commutatif (E, + ) muni d'une loi externe
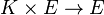
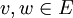
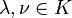
Un espace affine d'espace vectoriel directeur E est un ensemble A et d'une action libre et transitive du groupe commutatif (E, + ) sur A.
Les espaces affines sont des plans affines de Désargues.
Réciproque
Réciproquement, tout plan affine de Désargues P est un espace affine dont l'espace vectoriel directeur est le groupe de translations de P.
Si T est la translation envoyant O sur O', la conjugaison d'une homothétie de centre O' par la translation T est une homothétie de centre O. Par suite, la conjugaison par T induit un isomorphisme :
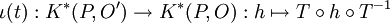
Ces isomorphismes se composent les uns les autres :
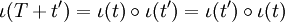
Par ailleurs, la conjuguée d'une translation par une homothétie est une translation. Par suite, la conjugaison par une homothétie induit un isomorphisme :
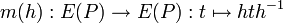
Pour toute translation t et pour toute homothétie h, on a :
Le corps des scalaires est défini comme l'ensemble contenant un élément privilégié 0 et les classes d'homothéties définies à conjugaison près par une translation. Les lois sont uniquement définies de sorte que :
- 0 soit l'élément neutre de la loi d'addition et (la classe réduite à) l'identité, notée 1, est l'élément neutre pour la loi de multiplication ;
- Le produit des classes de deux homothéties de centre O est la classe de leur composition ;
- La somme des classes de deux homothéties de centre O envoyant un point A respectivement sur B et C est la classe de l'homothétie de centre O envoyant A sur l'image de B par la translation envoyant O sur B.
- Volontairement, on ne fait pas de différence entre une homothétie et sa classe de conjugaison par des translations. Soient trois translations h, k et l de même centre O.
- Par définition, (h + k) est l'unique homothétie envoyant A sur l'image de h(A) par l'unique translation T envoyant O sur k(A). Le produit l.(h + k) est l'unique homothétie de centre O envoyant A sur l[T(h(A))].
- La transformation (lh + lk) est l'unique homothétie de centre O envoyant A sur l'image de lh(A) par l'unique translation T' envoyant O sur lk(A).
- En nommant M = h(A) et N = k(A), la translation T'' = T' − 1 est l'unique translation envoyant l(N) sur le centre O de l'homothétie l ; la translation T est (par définition) l'unique translation envoyant O sur N. Alors
-
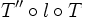
![T''\circ l\circ T(O)=T''\left[l(N)\right]=O](https://static.techno-science.net/illustration/Definitions/autres/8/8a8d2c8c5f44d88e4b33093b83e972bc_a2e2c15f80051fdac087c8c3d7909bbf.png)
-
- Par suite, comme le centre O et l'image l(N) de N déterminent uniquement l'homothétie l, il vient :
-
-
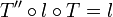
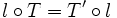
- En évaluant en h(A), il vient :
- l[T(h(A))] = T'[lh(A)].
- Les homothéties l(h + k) et lh + lk sont les uniques homothéties de centre O envoyant A respectivement sur l[T(h(A))] et T'[lh(A)]. Elles sont donc égales.
![T''\circ l\circ T(O)=T''\left[l(N)\right]=O](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/8a8d2c8c5f44d88e4b33093b83e972bc_a2e2c15f80051fdac087c8c3d7909bbf.png)
(Vérifications à faire, dessins, ...)
