Plan affine de Desargues - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans une approche axiomatique de la géométrie, un plan affine de Desargues est un plan affine incident P vérifiant l'axiome de Desargues :
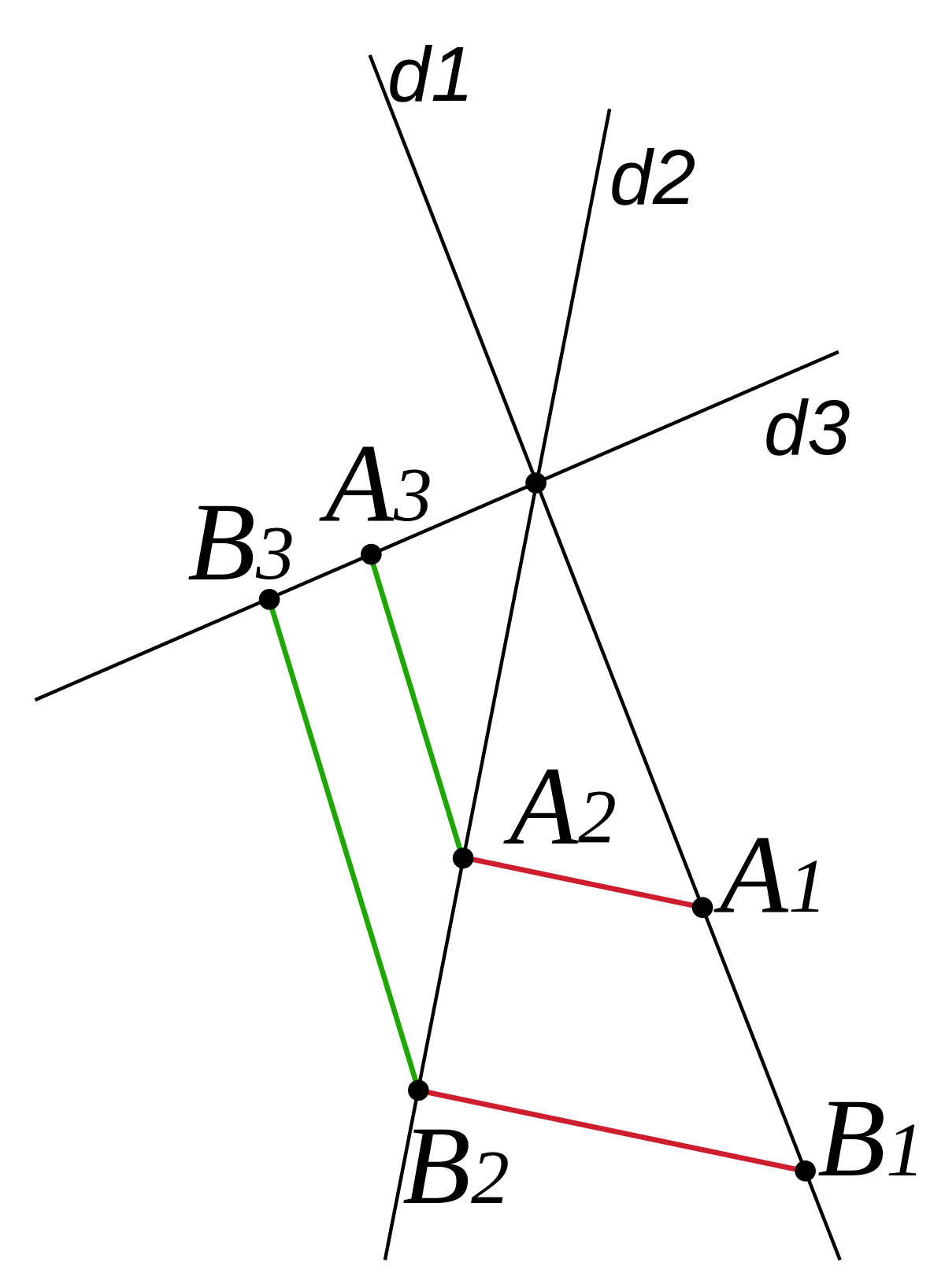
- Pour toutes droites d1, d2 et d3 concourantes ou deux à deux parallèles, et pour tous points A1 et B1 incidents à d1 ; A2 et B2 incidents à d2 ; A3 et B3 incidents à d3, si deux des trois couples de droites (A1A2) et (B1B2) ; (A2A3) et (B2B3) ; (A1A3) et (B1B3) sont des couples de droites parallèles, alors le troisième l'est aussi.
Cet axiome permet la définition des homothétie et de translation. De plus, il permet de définir axiomatiquement la structure de plan affine. Plus précisément, tout plan de Désargues se réalise comme un plan affine sur un corps K (non nécessairement commutatif), dont l'espace vectoriel directeur n'est autre que l'ensemble des translations du plan ; le groupe multiplicatif de K s'identifie au groupe des homothéties de centre un point donné O. Réciproquement, tout plan affine, défini comme sous-espace affine de dimension 2 sur un corps K, satisfait les axiomes d'incidence et l'axiome de Desargues.
On obtient le même résultat pour les plan affine sur un corps commutatif en ajoutant, en plus de l'axiome de Desargues l'axiome de Pappus.
Définition d'une homothétie-translation (dans un plan affine incident)
Une homothétie-translation est par définition une bijection h de l'ensemble des points d'un plan affine incident P telle que les deux conditions suivantes sont satisfaites :
- La transformation h préserve l'alignement des points. Autrement dit, h envoie trois points alignés sur trois points alignés. En particulier, h envoie tout point incident à une droite d sur des points incidents à une même droite, notée h(d). L'application h induit alors une bijection de l'ensemble des droites de P sur lui-même.
- La transformation h envoie toute droite sur une droite qui lui est parallèle.
- Considérons une bijection h de l'ensemble des points de P préservant l'alignement et envoyant toute droite sur une droite qui lui est parallèle. Supposons que h fixe deux points distincts, O et A.
- Pour tout point M non incident à la droite (OA), la transformation h envoie la droite (OM) sur une droite contenant h(O) = O qui lui est parallèle. Par les axiomes d'incidence, cette droite est donc confondue à (OM) ; donc h(M) est incident à la droite (OM). De même, il est incident à la droite (AM). Par suite, h(M) est le point d'intersection des droites (OM) et (AM) ; il est donc confondu au point M. On a montré que h fixe tous les points non incidents à (OA).
- Si N est un point incident à (OA), les axiomes d'incidence impliquent l'existence d'un point B non incident à (OA). Par ce qui précède, la transformation h fixe B, et par hypothèse, elle fixe O. Le même raisonnement que ci-dessus appliqués aux trois points non alignés O, B et N prouve que h fixe N.
- De fait, la transformation h fixe tous les points de P, c'est l'identité.
Si la transformation h diffère de l'identité :
- Ou bien h ne fixe aucun point du plan P, auquel cas h est appelée translation ;
- Ou bien h fixe un unique point O, auquel cas h est appelée homothétie de centre O.
L'identité est considérée à la fois comme une translation et une homothétie. Le centre d'une homothétie non triviale (ie une homothétie différente de l'identité) est uniquement défini.
La définition d'une homothétie-translation ne s'appuie que sur les axiomes d'incidence.
Détermination d'une homothétie-translation (dans un plan affine de Désargues)
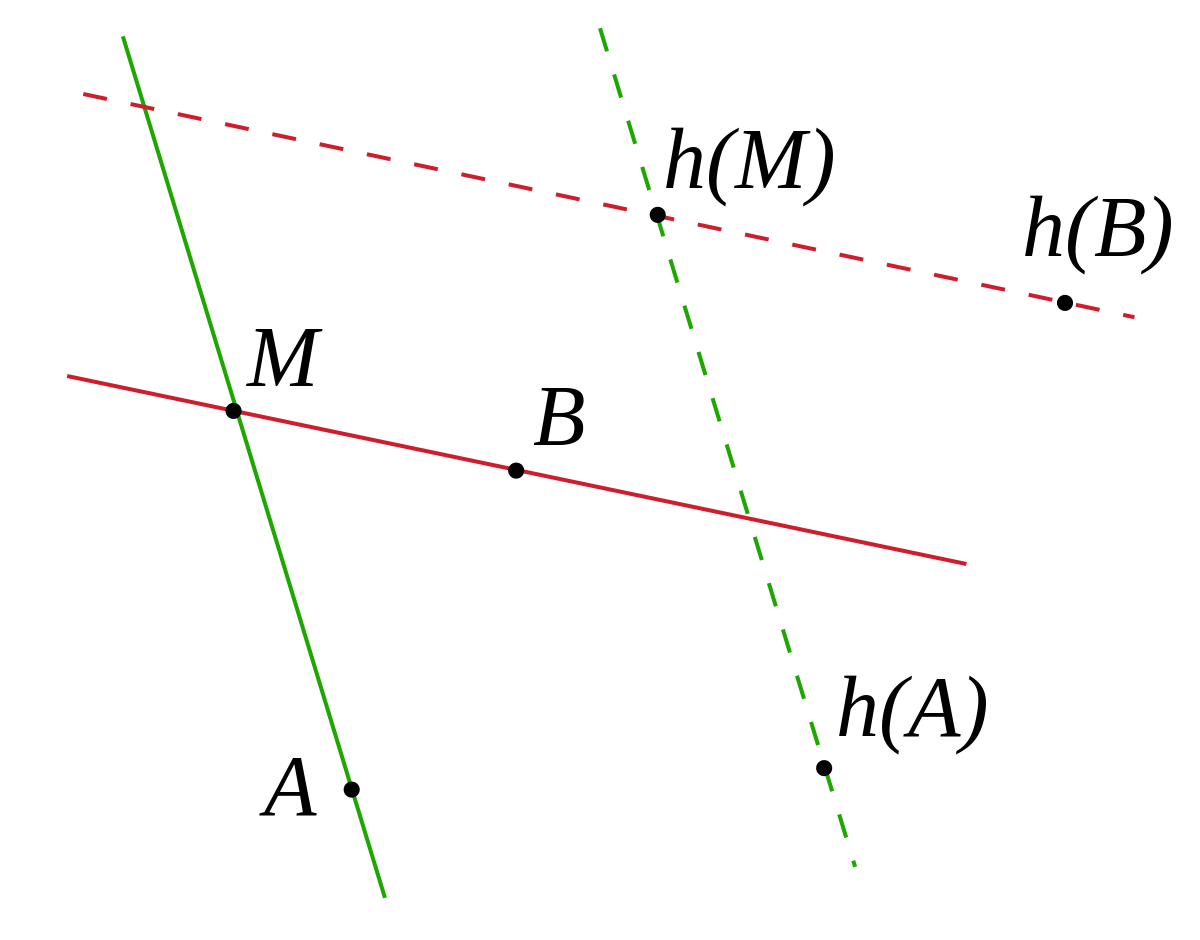
Dans un plan affine incident P, une homothétie-translation h est uniquement déterminée par les images h(A) et h(B) de deux points distincts A et B. Plus précisément, comme h envoie toute droite sur une droite qui lui est parallèle, l'image d'un point M non incident à la droite (AB) se définit uniquement comme le point d'intersection de la parallèle à (AM) passant par h(A) et de la parallêle à (BM) passant par h(B). L'image d'un point incident à (AB) se détermine par une construction analogue à partir de l'image de A et d'un point non incident à (AB) dont l'existence est assurée par les axiomes d'incidence.
Pour quatre points A, B, A' et B', l'existence d'une homothétie-translation envoyant A sur A' et B sur B' implique que les droites (AB) et (A'B') soient parallèles. Cependant, en l'absence de l'axiome de Désargues, même si cette condition nécessaire est validée, l'existence d'une telle homothétie-translation n'est pas assurée.
- Dans un plan affine de Désargues, la donnée de quatre points A, B, A' et B' déterminent une unique homothétie-translation envoyant A sur A' et B sur B' si et seulement si les droites (AB) et (A'B') sont parallèles.
Définissons une bijection h de l'ensemble des points du plan affine de Désargues P :
- Les images h(A) et h(B) sont par définition les points A' et B'.
- L'image h(M) d'un point M non incident à la droite (AB) est défini comme le point d'intersection de la parallèle à (AM) passant par h(A) et de la parallèle à (BM) passant par h(B).
- Fixons un point C non incident à la droite (AB) dont l'existence est assurée par l'un des axiomes d'incidence. L'image h(N) d'un point N incident à la droite (AB) est défini comme le point d'intersection de la parallèle à (CN) passant par h(C) et de la droite (A'B').
.............
Détermination de la nature d'une homothétie-translation
La nature de la transformation peut être précisée dans le cas où les quatre points A, B, h(A) et h(B) sont non tous alignés. Cette hypothèse implique
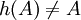
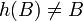
- Ou bien les droites (Ah(A)) et (Bh(B)) s'intersectent en un unique point O, et dans ce cas, h est une homothétie de centre O ;
- Ou bien les droites (Ah(A)) et (Bh(B)) sont parallèles, et dans ce cas, h est une translation.
Le résultat précédent peut être amélioré si on connait a priori la nature de l'homothétie-translation :
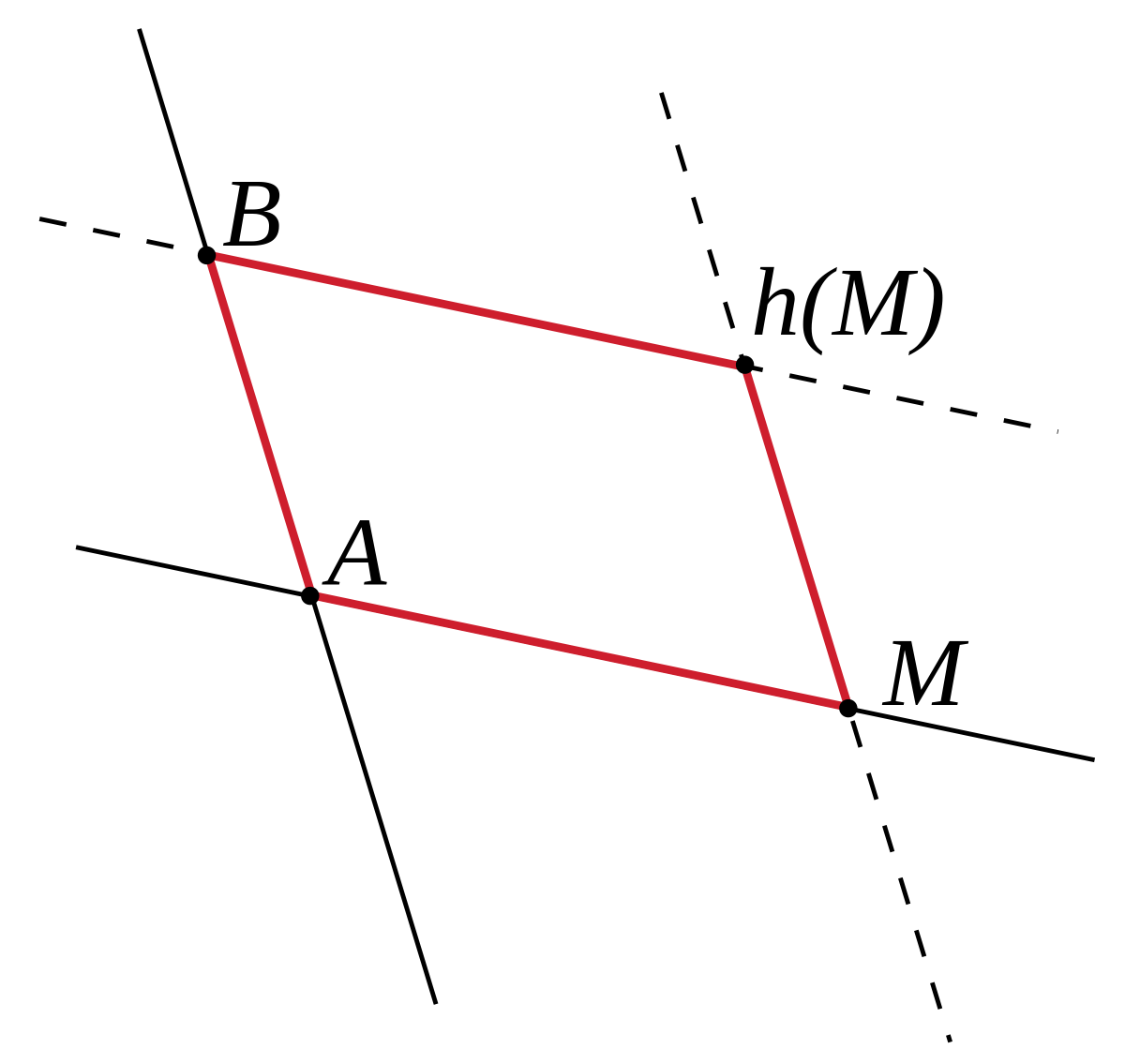
- Une translation non triviale du plan de Désargues est uniquement définie par l'image d'un point, donc par la donnée de deux points distincts. Si une translation envoie A sur B, alors elle envoie un point M non incident à (AB) sur le point d'intersection de la parallèle à (AB) passant par M et de la parallèle à (AM) passant par B. L'image d'un point N incident à (AB) se détermine par l'intermédiaire d'un point non incident à (AB). Les figures suivantes précisent la construction :
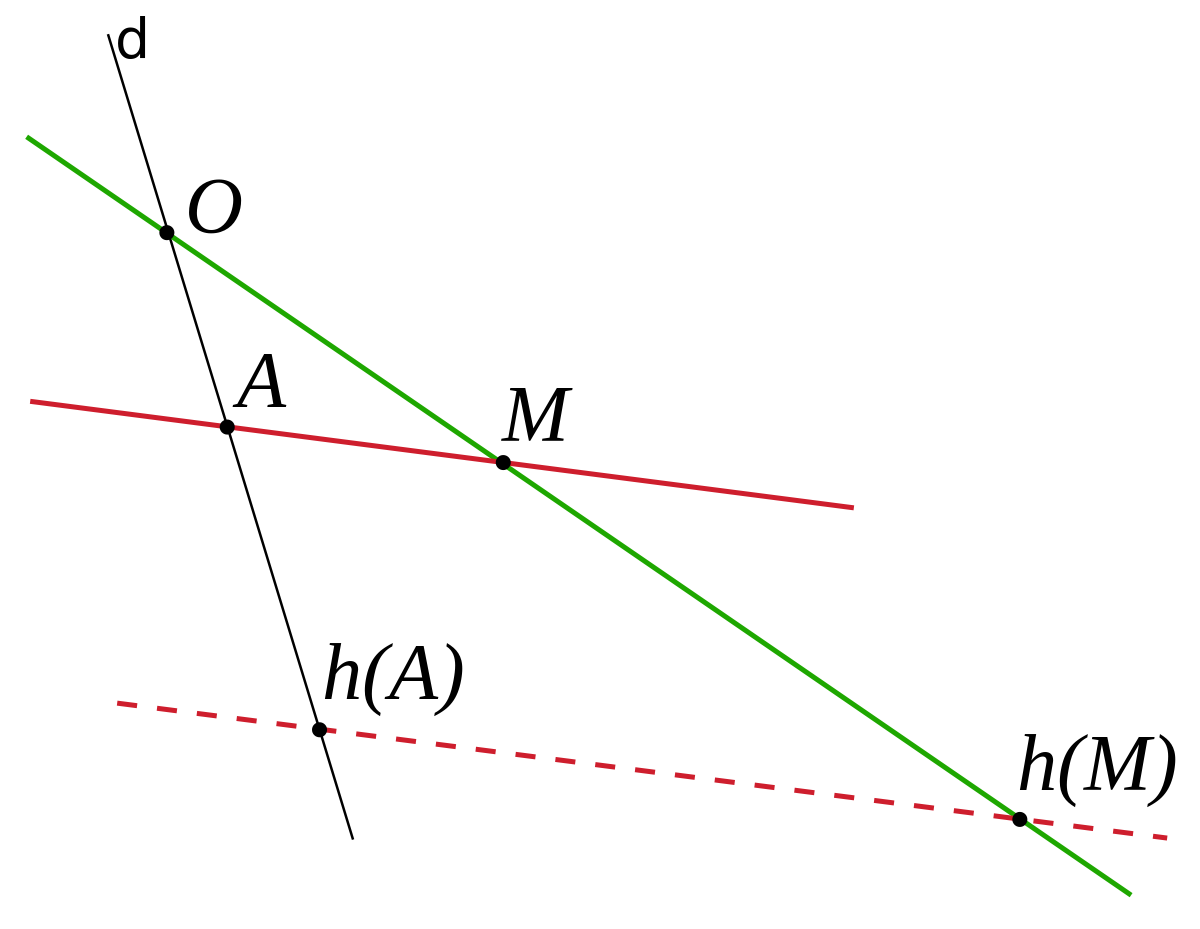
- Une homothétie non triviale du plan de Désargues est uniquement définie par son centre O et l'image h(A) d'un point A qui lui est distinct, donc par trois points distincts alignés. L'image d'un point M non incident à (OA) est définie comme le point d'intersection de la droite (OM) et de la parallèle à (AM) passant par h(A). L'image d'un point incident à la droite (OA) se définit par l'intermédiaire d'un point non incident. Les figurent suivantes précisent les constructions :
Composition
L'ensemble des homothéties-translations est stable par composition et l'inverse d'une homothétie-translation est une homothétie translation. En effet, si deux bijections de l'ensemble des points de P préservent l'alignement et envoie une droite sur une droite qui lui est parallèle, il en va de même de leurs composées. Cet ensemble forme donc un sous-groupe du groupe des bijections de l'ensemble des points de P, noté G :
L'ensemble des translations d'un pman affine de Désargues forme un sous-groupe de G, noté E(P) :
- L'inverse d'une translation est une translation. Un éventuel point fixe de l'inverse serait un point fixe de la translation T, ce qui est absurde si la translation est non triviale, par définition. Donc, l'inverse T − 1 est une translation.
- La composée de deux translations est une translation. La composée
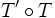
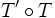
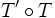
- Soient deux translations T et T' d'un plan affin de Désargues. Soit M un point quelconque de P. En nommant A = T'(M), les points A et T(A) déterminent uniquement l'image T(M) de M par la translation T. On suppose pour simplifier que les points M, A et T(A) sont non alignés. Le point T(M) est le point d'intersection de la parallèle à (AT(A)) passant par M et de la parallèle à (AM) passant par T(A).
- De manière analogue, l'image T'(M) de M détermine uniquement l'image de T(M) par T' : le point
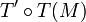
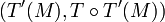
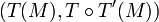
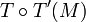
- Par suite, il vient :
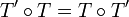
L'ensemble des homothéties de centre O forme un sous-groupe de G, noté K * (P,O) :
- L'inverse d'une homothétie de centre O est une homothétie-translation dont O est un point fixe ; donc une homothétie de centre O ;
- Pour les mêmes raisons, la composée de deux homothéties de même centre O est une homothétie de centre O.
- Le groupe des homothéties de centre 0 n'est pas en général commutatif. celle-ci dépend d'un axiome supplémentaire, la propriété de Pappus (version affine).