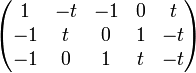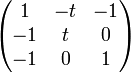Polynôme d'Alexander - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en théorie des nœuds, le polynôme d'Alexander est un invariant (topologique) qui associe un polynôme à coefficients entiers à chaque type de nœud. C'est le premier polynôme de nœud découvert ; il l'a été par James Waddell Alexander II, en 1923. En 1969, John Conway en montra une version, appelée à présent le polynôme d'Alexander-Conway, pouvant être calculé à l'aide d'une « relation d'écheveau » (skein relation), mais l'importance n'en fut pas comprise avant la découverte du polynôme de Jones en 1984.
Définition
La définition formelle suivante nécessite des connaissances importantes en homologie ; il est cependant possible, comme on le verra au paragraphe suivant, de calculer sans elles le polynôme d'Alexander en pratique, ce qui pourrait en constituer une définition opérationnelle, mais on ne peut alors comprendre la raison profonde de l'intérêt de ce calcul, ni les propriétés du polynôme.
Soit K un nœud de la 3-sphère. Soit X le recouvrement cyclique infini du complémentaire du nœud K. Il y a une transformation couvrante t agissant sur X. Soit alors H1(X) le premier groupe d'homologie (à coefficients entiers) de X. La transformation t agit sur ce groupe, et nous pouvons donc considérer H1(X) comme un module sur
![\mathbb{Z}[t, t^{-1}]](https://static.techno-science.net/illustration/Definitions/autres/e/eaf23549827bb1cb5739c19ff8b5dd30_a407a416cec04c3c637c06d94c12de5f.png)
Ce module est de présentation finie ; une matrice de présentation de ce module s'appelle une matrice d'Alexander. Si le nombre de générateurs, r, est inférieur ou égal au nombre de relations, s, alors l'idéal engendré par tous les r l'est par r mineurs de la matrice ; c'est l'idéal d'Alexander, et il ne dépend pas du choix de la matrice de présentation.
Si r > s, on prend l'idéal nul. Si l'idéal d'Alexander est principal, un de ses générateurs est appelé polynôme d'Alexander du nœud. Ce polynôme n'étant défini qu'à une multiplication près, par le monôme de Laurent
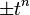
Alexander démontra que l'idéal d'Alexander est en fait toujours principal et non nul. Ainsi, le polynôme d'Alexander existe toujours, et est clairement un invariant (topologique) de nœud, que l'on note ΔK(t).
Propriétés élémentaires
Le polynôme d'Alexander est symétrique : ΔK(t − 1) = ΔK(t).
- Du point de vue de la définition formelle, ceci exprime l'isomorphisme de la dualité de Poincaré :
![\overline{H_1 X} \simeq \mathrm{Hom}_{\Bbb Z[t,t^{-1}]}(H_1 X, G)](https://static.techno-science.net/illustration/Definitions/autres/1/1a5bc0797e7893f333da550e5b0592cd_4b60e23bd7f47c2a5ad2ced5d9d1fc9b.png)
![\Bbb Z[t,t^{-1}]](https://static.techno-science.net/illustration/Definitions/autres/a/aa5283c0406939a171b2272d192ac5c8_3d1c6184d2d4c3ce3301c9179970dc09.png)
![\Bbb Z[t,t^{-1}]](https://static.techno-science.net/illustration/Definitions/autres/a/aa5283c0406939a171b2272d192ac5c8_3d1c6184d2d4c3ce3301c9179970dc09.png)
![\Bbb Z[t,t^{-1}]](https://static.techno-science.net/illustration/Definitions/autres/a/aa5283c0406939a171b2272d192ac5c8_3d1c6184d2d4c3ce3301c9179970dc09.png)
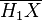
![\Bbb Z[t,t^{-1}]](https://static.techno-science.net/illustration/Definitions/autres/a/aa5283c0406939a171b2272d192ac5c8_3d1c6184d2d4c3ce3301c9179970dc09.png)
Le polynôme d'Alexander vaut 1 ou -1 pour t = 1.
- Ceci exprime le fait que le complémentaire du nœud est homologue à un cercle, engendré par la transformation couvrante t. Plus généralement, si M est une variété de dimension 3 telle que rank(H1M) = 1, elle possède un polynôme d'Alexander ΔM(t) défini comme un idéal de son recouvrement, et alors ΔM(1) est égal à l'ordre du sous-groupe de torsion de H1M.
Réciproquement, tout polynôme de Laurent (à coefficients entiers), symétrique et valant
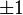
Calcul du polynôme
La procédure de calcul suivante est celle qui fut donnée par Alexander dans sa publication originale.
Considérons un diagramme orienté du nœud avec n croisements ; le diagramme partage le plan en n + 2 régions (c'est une conséquence facile de la relation d'Euler). Pour déterminer le polynôme d'Alexander, on construit d'abord une matrice d'incidence de taille (n, n + 2). Les n rangées correspondent aux n croisements, et les n + 2 colonnes aux régions. Considérons l'entrée correspondant à une région et à un croisement particulier. Si la région n'est pas adjacente au croisement, cette entrée vaut 0. Sinon, la table suivante donne la valeur de l'entrée compte tenu de la position de la région vue du point de vue de la ligne entrante passant par dessous l'autre :
- à gauche avant le croisement : −t
- à droite avant le croisement : 1
- à gauche après le croisement : t
- à droite après le croisement : −1
En supprimant alors de la matrice deux colonnes correspondant à des régions adjacentes, on obtient une nouvelle matrice d'ordre n ; son déterminant (à un facteur
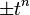
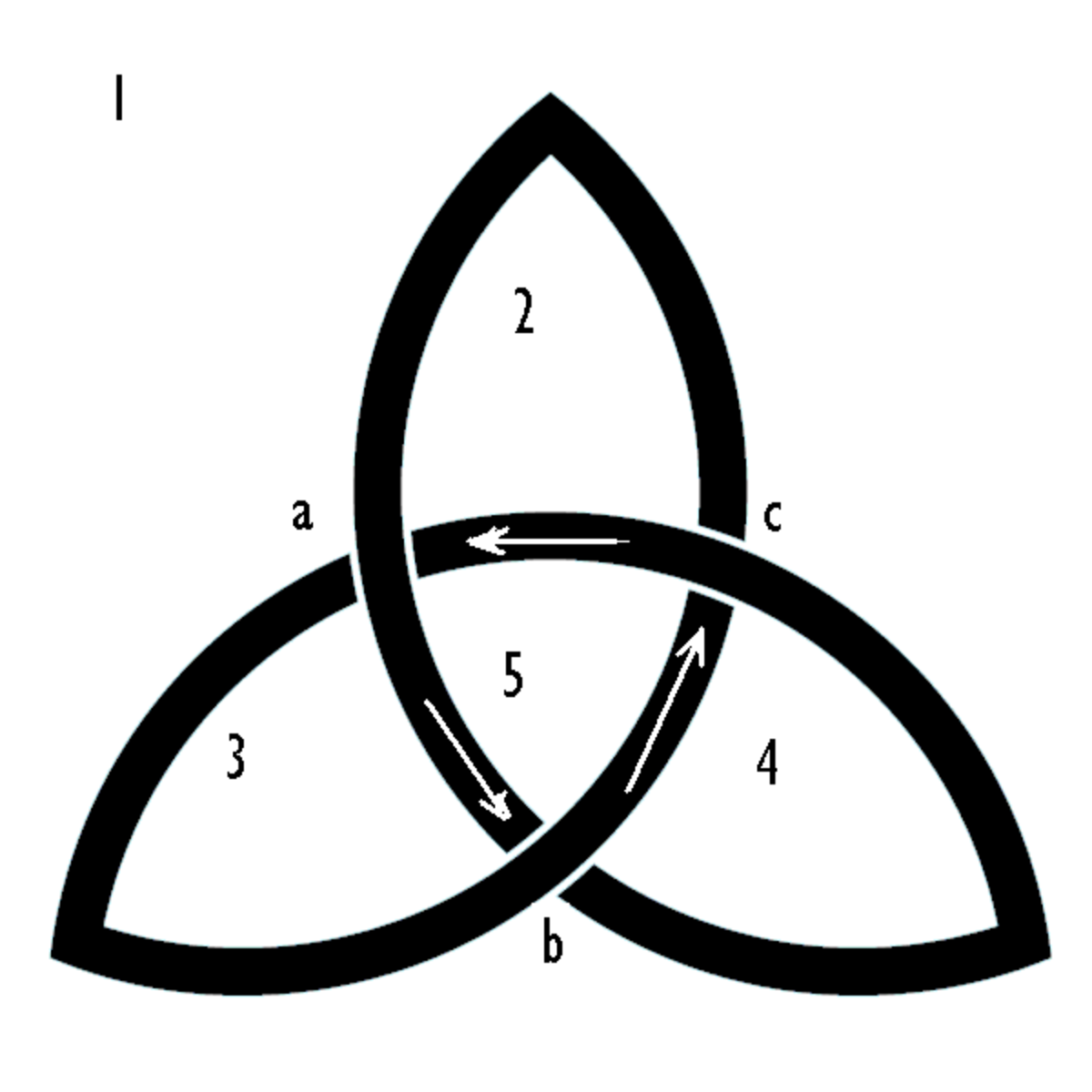
Le calcul correspond au diagramme ci-contre (cliquer sur l'image pour une meilleure visualisation) :
La matrice d'incidence est :
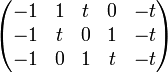
(dont les cinq colonnes correspondent respectivement aux régions 1 à 5, et les trois lignes aux croisements a, b et c).
En supprimant les deux dernières colonnes (correspondant aux deux régions adjacentes 4 et 5), on obtient
-
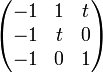
Le même diagramme, en remplaçant le croisement en a par son opposé, donne un nœud trivial (équivalent à un cercle), une matrice d'incidence qui devient :