Polynôme d'Alexander - Définition

Relations avec les opérations sur les nœuds satellites

Si un nœud K est un nœud satellite de compagnon K', c'est-à-dire s'il existe un plongement tel que K = f(K'), où est un tore plein non noué, alors , où est l'entier représentant dans .

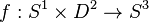
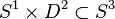
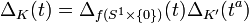
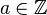
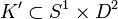
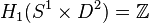
Par exemple, pour une somme jointe . Si K est une paire de Whitehead sans torsion, alors .

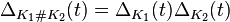
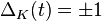
Interprétations géométriques

Comme l'idéal d'Alexander est principal, Δ_K(t) = 1 si et seulement si le sous-groupe des commutateurs du groupe du nœud (le groupe fondamental du complémentaire du nœud dans R³) est parfait (égal à son propre sous-groupe de commutateurs). C'est évidemment en particulier le cas du nœud trivial (le cercle), mais ce résultat montre que le calcul du polynôme d'Alexander ne suffit pas pour montrer qu'un nœud est trivial en général.

Pour un nœud tranche, c'est-à-dire un nœud de la 3-sphère qui borne un disque "localement plat" de la 4-boule, le polynôme d'Alexander satisfait la condition de Fox-Milnor Δ_K(t) = f(t)f(t ^{− 1}), où f(t) est un autre polynôme de Laurent (à coefficients entiers).

Réciproquement, Michael Freedman a démontré que si le polynôme d'Alexander d'un nœud est trivial, ce nœud est un nœud tranche (Freedman et Quinn, 1990).

Le degré du polynôme d'Alexander est supérieur ou égal au double du genre du nœud.

Il y a d'autres relations avec les surfaces et la topologie (différentielle) en dimension 4. Par exemple, sous certaines hypothèses, il y a moyen de modifier une variété différentielle de dimension 4 par un acte chirurgical consistant à retirer un voisinage d'un tore (à deux dimensions) et à le remplacer par le produit du complémentaire d'un nœud et deS¹. Le résultat est une variété homéomorphe à la variété initiale, mais dont l'invariant de Seiberg-Witten a été multiplié par le polynôme d'Alexander du nœud.

Le fait qu'un nœud présente une symétrie se traduit en général par des propriétés particulières de son polynôme d'Alexander. Cependant, celui-ci ne permet pas de les détecter toutes ; c'est le cas de l'invertibilité forte.

Si le complémentaire du nœud est un fibré à base circulaire, on peut montrer que le polynôme d'Alexander est monique (les termes de plus haut et plus bas degré valent ). En fait, si est un fibré, où C_K est le complémentaire du nœud ; notons la monodromie. Alors Δ_K(t) = Det(tI − g _* ), où est l'application induite sur les classes d'homologie.

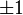
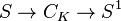
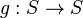
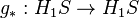
Le polynôme d'Alexander-Conway

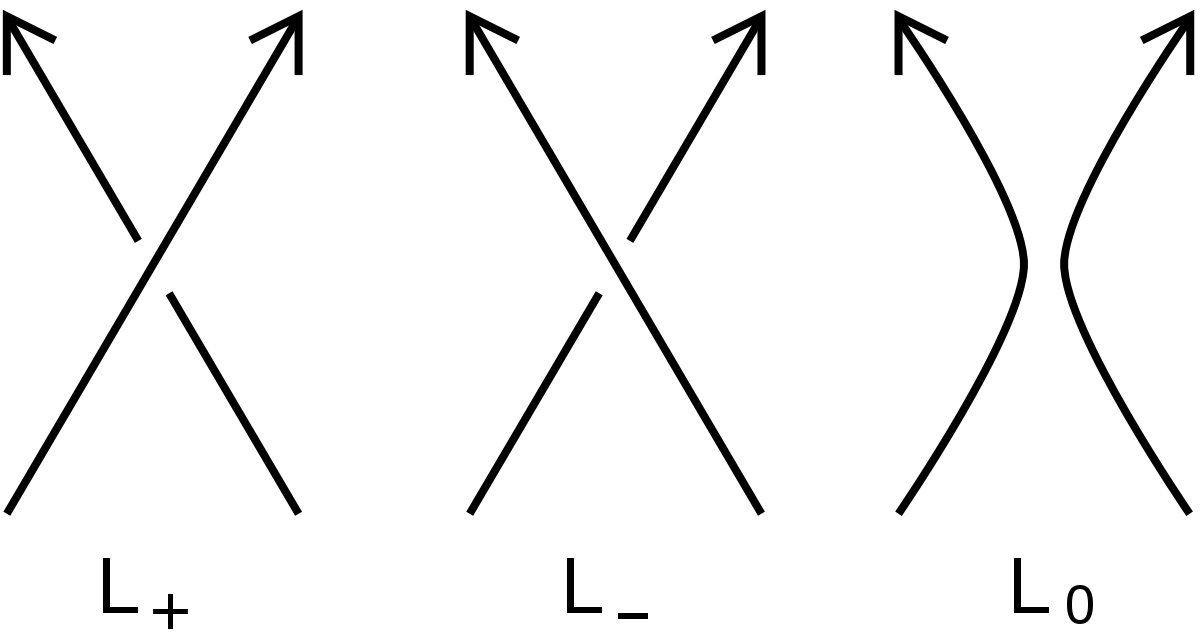
Alexander avait démontré que le polynôme d'Alexander satisfait une relation d'écheveau. Cela fut redécouvert par John Conway sous une forme différente, montrant que cette relation, et un choix convenable de valeurs sur le transformé (dénoué) suffit à déterminer le polynôme. Le résultat de la version de Conway est un polynôme en z à coefficients entiers, noté et appelé le polynôme d'Alexander-Conway.

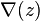
Soit L un diagramme orienté d'un nœud ; on note les diagrammes résultant d'un changement limité à une petite région autour d'un croisement spécifié, comme indiqué sur la figure.

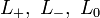
Les relations d'écheveau (skein relations) de Conway sont les suivantes :

• (où O est n'importe quel diagramme non noué)
• 

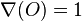
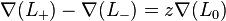
La relation avec le polynôme d'Alexander standard est donnée par . Ici, Δ_L doit être convenablement normalisé (par multiplication par ) pour satisfaire la relation d'écheveau Δ(L ₊ ) − Δ(L ₋ ) = (t^{1 / 2} − t ^{− 1 / 2})Δ(L₀). Il faut remarquer que cette relation donne un polynôme de Laurent en t^1/2.

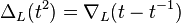
Peu de temps après que Conway ait montré ces relations, on se rendit compte qu'une relation similaire avait été décrite par Alexander dans sa publication originale.