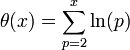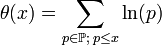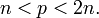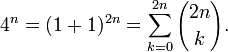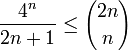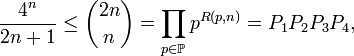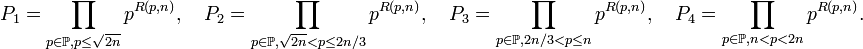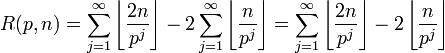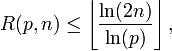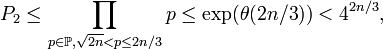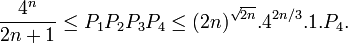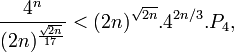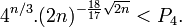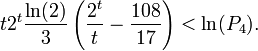Postulat de Bertrand - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le postulat de Bertrand, aussi appelé théorème de Tchebychev, affirme qu'entre un entier et son double existe toujours un nombre premier. Plus formellement, si n est un entier naturel supérieur ou égal à 2, alors il existe toujours au moins un nombre premier p tel que
- n < p < 2n
Bien que démontré, il a gardé son nom de postulat, c'est-à-dire une conjecture.
Historique
Cette affirmation fut pour la première fois conjecturée en 1845 par Joseph Bertrand qui la vérifia lui-même pour tous les nombres de l'intervalle
![[2 ; 3 \times 10^6]](https://static.techno-science.net/illustration/Definitions/autres/f/fd6034cfcff6a857a4c3a89a66263c17_6062d91229c4b1c23481d31a8e6d6d0b.png)
Ramanujan donna une démonstration plus simple et Paul Erdős en 1932 publia une preuve très simple dans laquelle il utilisa les coefficients binomiaux et la fonction θ, définie par:
où p parcourt les nombres premiers inférieurs ou égaux à x.
Démonstration
Notons
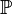
Voici le plan de la démonstration :
- lemme de majoration de θ(x),
- vérification explicite de la propriété pour n ≤ 630,
- démonstration de la propriété pour n > 630 (en utilisant le lemme).
Lemme de majoration de θ(x)
Pour tout entier .
Démonstration du lemme, par récurrence
- La propriété est vraie pour n = 1 :
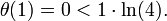
- Soit N>1. Supposons la majoration vraie pour tous les entiers positifs n<N et montrons-la pour n=N.
- Si N=2 :
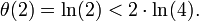
- Si N > 2 et N est pair :
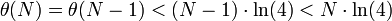
- Si N=2 :
- (parce que N, étant pair et différent de 2, n'est pas premier, donc il y a autant de nombres premiers entre 1 et N qu'entre 1 et N-1).
-
- Si N est impair. Soit N = 2m+1 avec m > 0. Par la formule du binôme de Newton,
-
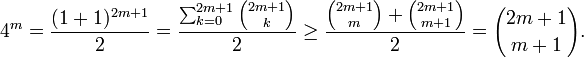
- Chaque nombre premier p tel que m+1 < p ≤ 2m+1 divise
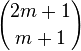
-
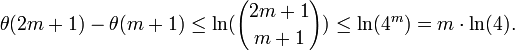
- Par hypothèse de récurrence,
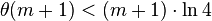
-
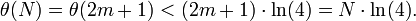
CQFD
Vérification pour n ≤ 630
Si 2 ≤ n ≤ 630, on utilise le procédé de Landau :
considérons la suite de onze nombres premiers 2, 3, 5, 7, 13, 23, 43, 83, 163, 317 et 631, chacun étant strictement inférieur au double de son prédécesseur.
Il existe deux nombres consécutifs de cette liste, q et p, tels que
-
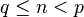
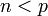
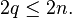
De plus, par construction de cette liste,
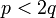
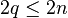
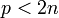
Preuve pour n > 630
- Mise en place de la stratégie
Par la formule du binôme,
Puisque
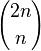
Appelons R(p,n) le plus grand nombre x tel que px divise
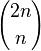
avec
Pour minorer P4 (afin de montrer que P4 > 1), on va majorer
- Calcul des R(p,n)
On désigne par
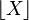
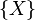
Puisque (d'après un théorème de Legendre) n! possède
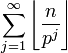
- Majoration de P1
Puisque chaque terme
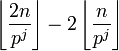
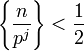
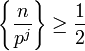
 sont nuls, on obtient :
sont nuls, on obtient :
donc
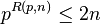
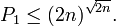
- Majoration de P2
Pour  , la somme dans R(p,n) est réduite à son premier terme,
, la somme dans R(p,n) est réduite à son premier terme,
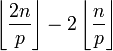
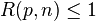
la dernière inégalité venant du lemme.
- Majoration de P3
En fait, P3 = 1 (c'est le point clé de la preuve d'Erdös) car si
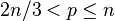
-
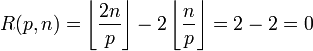
- Synthèse
On aboutit à
On obtient un minorant plus commode en remarquant que 2n + 1 < (2n)2 et que
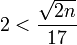
qui se réécrit
En prenant les logarithmes et en remplaçant 2n par 22t :
Or 2n > 1024 = 210 donc t > 5, d'où  , si bien que ln(P4) > 0, ce qui achève la preuve.
, si bien que ln(P4) > 0, ce qui achève la preuve.