Principe de correspondance - Définition

Autres acceptions

Dès 1915, Einstein utilisait un principe de substitution pour passer des équations de la relativité restreinte à celle de la relativité générale, et pour s'aider à déterminer les équations du champ de gravitation.

Par ailleurs, le terme de « principe de correspondance » est également repris dans un sens plus philosophique, selon lequel une nouvelle théorie scientifique englobant une théorie précédente doit pouvoir expliquer tout ce que cette dernière expliquait.

Par exemple, la théorie de la relativité restreinte satisfait ce principe : à des vitesses plus faibles devant celle de la lumière, on retrouve la mécanique classique. De même, la relativité générale donne la mécanique classique pour des champs gravitationnels faibles.

En relativité générale

Einstein comprit qu'en relativité restreinte la dérivation suivant un axe de coordonnée est remplacée, en relativité générale, par la dérivation covariante qui consiste à dériver suivant le substitut à la notion de droite dans un espace courbe : le chemin suivi par le mouvement inertiel, ce que l'on appelle une géodésique.
C'est une application du principe d'équivalence et du principe de relativité : les équations de la relativité restreinte sont vues comme des équations de tenseurs dans un référentiel inertiel (en mouvement suivant une géodésique, ou encore en chute libre dans le champ de gravitation), et pour retrouver les équations dans les autres référentiels, il suffit de remplacer chaque tenseur utilisé par son expression générale en relativité générale, et chaque dérivée suivant une droite du référentiel d'inertie, donc cette droite est une géodésique, par l'expression de la dérivation suivant cette géodésique.

Pour retrouver formellement les équations de la relativité générale à partir des équations de la relativité restreinte, il faut :

• S'assurer que l'équation de la relativité restreinte est bien une égalité de tenseurs. Par exemple la quadri-vitesse est un tenseur, mais les quadri-coordonnées n'en forment pas un.

• Y remplacer la métrique par la métrique .

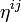
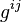
• Y remplacer les différentielles par les différentielles covariantes ou , suivant la notation choisie.

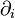
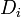
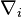
• Y remplacer, dans les intégrales, le volume élémentaire par .

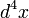
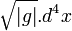
On obtient alors l'équation de la relativité générale qui concerne le même sujet que celui traité en relativité restreinte.

Bien sûr, on ne peut obtenir ainsi les équations du champ de gravitation qui ne peuvent être traitées en relativité restreinte. Toutefois, ce fut un guide précieux :

En relativité restreinte, le tenseur d'énergie vérifie , ce qui donne, en relativité générale, . Fort de l'idée que la gravitation est une déformation de la géométrie de l'espace due à l'énergie du corps présent, Einstein chercha donc un tenseur géométrique vérifiant la même égalité, pour pouvoir écrire , où est une constante homogénéisant les dimensions. Son ami Marcel Grossmann lui indiqua, vers 1912, que l'on pouvait prendre , ce qui laissa Einstein incrédule. En 1915, finalement, Einstein admit que c'était là le tenseur géométrique cherché, et par la suite, Élie Cartan démontra que c'était le seul vérifiant l'équation , à une constante additive près (qui donnera la constante cosmologique), et ne contenant que les dérivées premières et secondes des coefficients de la métrique de l'espace (condition signifiant que position, vitesse et accélération suffisent pour décrire l'évolution de tout système physique, ce qui est une hypothèse héritée de Newton).

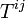
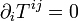
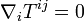
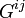
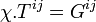
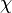
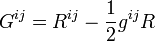
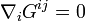
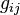
Mais l'histoire précise de la découverte de la relativité générale est riche de détails scientifiques et humains, et est sujet à controverses.

Exemple : énergie cinétique relativiste

On montre ici comment l'expression relativiste de l'énergie cinétique, dans le cadre de la relativité restreinte, est approximativement égale à l'énergie cinétique classique quand la vitesse est très inférieure à celle de la lumière.

On part de l'équivalence célèbre d'Einstein :

Pour l'énergie quand le corps est au repos par rapport à l'observateur

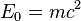
Pour l'énergie quand le corps se déplace à la vitesse v par rapport à l'observateur

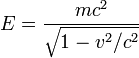
Quand la vitesse par rapport à l'observateur est non nulle, l'énergie dépasse l'énergie au repos d'une quantité définie comme étant l'énergie cinétique :

On retrouve bien l'expression classique de l'énergie cinétique.