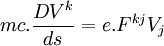Principe de moindre action et relativité générale - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
On doit à David Hilbert, en 1915, la première utilisation du principe de moindre action pour obtenir les équations de la relativité générale, notamment les équations du champ gravitationnel.
Pour la relativité générale, comme pour la relativité restreinte, les équations peuvent être obtenues sans faire appel au principe de moindre action : le principe d'équivalence, exprimé sous la forme « on peut toujours trouver un référentiel annulant localement le champ de gravitation », permet de retrouver directement les équations du mouvement d'une particule ; et l'unicité de la forme du tenseur géométrique qui s'annule par la dérivée covariante, unicité prouvée par Élie Cartan, permet de trouver les équations du champ de gravitation, ce qui fût la méthode originelle d'Einstein (bien que l'unicité en question n'était pas encore prouvée à l'époque).
Si les équations de la relativité générale sont données, on peut en déduire l'action permettant d'appliquer le principe. En particulier, avec les équations des géodésiques on peut retrouver la métrique
Particule
Particule dans un champ de gravitation
Dans ce travail, on utilise l'hypothèse que la particule ne modifie pas son environnement : la masse de la particule ni sa position ne changent le champ de gravitation, cette masse doit donc être « petite ».
En vertu du principe d'équivalence d'Einstein, la gravitation est localement équivalente au choix d'un référentiel accéléré.
Dans le cadre de la relativité restreinte, en prenant un référentiel accéléré (coordonnées
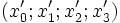
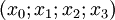
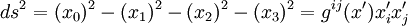
Le principe d'équivalence permet de dire qu'un champ gravitationnel réel (non dû au choix du référentiel) est aussi déterminé par la métrique
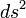
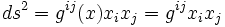
On peut donc rester dans la continuité de la relativité restreinte, et affirmer que l'action infinitésimale d'une particule ponctuelle, influencée par la seule gravitation, en relativité générale est :
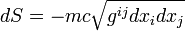
où on suppose que
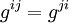
En utilisant le fait que
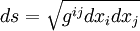
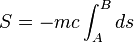
Pour garder la cohérence physique, on a besoin de supposer que les
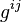
En considérant un temps t0 quelconque :
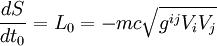
On utilise toujours les équations d'Euler-Lagrange
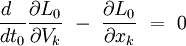
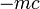
On obtient :
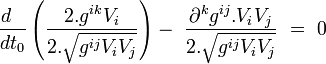
En prenant dès maintenant t0 = temps propre, on peut utiliser l'égalité
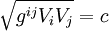
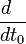
sans changer le résultat si on dérive avant, et on obtient
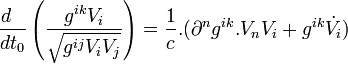
En remarquant que
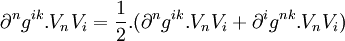
Les équations d'Euler-Lagrange donnent :
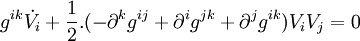
Avec l'égalité
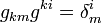
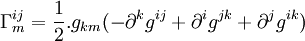
On obtient l'équation :
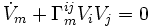
que l'on peut aussi écrire :
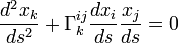
ou encore :
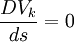
avec la « dérivée covariante » :
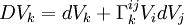
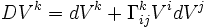
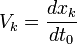
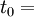
Le symbole de Christoffel
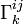
Les équations du mouvement ne dépendent pas de la masse de la particule (nommée ainsi car nous avons négligé son étendue spatiale et son influence sur son environnement) : toutes les particules suivent les mêmes trajectoires (à conditions initiales identiques), c'est l'équation des géodésiques en relativité générale, en présence de la seule gravitation.
Toutefois, ces équations du mouvement ne sont pas valables pour une particule de masse nulle car dans ce cas, on a dès le départ
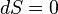
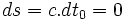
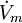
Particule dans un champ électromagnétique
De manière similaire à la relativité restreinte, la définition de l'action relativiste infinitésimale d'une particule ponctuelle de charge

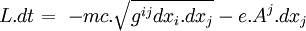
Par des calculs parfaitement similaires, on en tire les équations du mouvement :
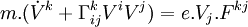
que l'on peut écrire :
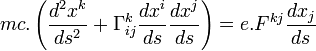
ou encore :