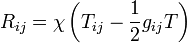Principe de moindre action et relativité générale - Définition
La liste des auteurs de cet article est disponible ici.
Champ de gravitation
Afin d'en déterminer la densité lagrangienne, puis les équations, il est nécessaire de développer un peu certaines considérations abordées ci-dessus, et même quelques nouvelles.
Densité lagrangienne dans l'espace courbe
Du fait de l'invariance de la trajectoire du champ par rapport aux référentiels d'où on l'observe, l'action qui la caractérise
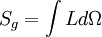
Soient
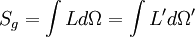
On a :
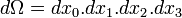
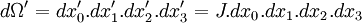
où
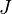
On a :
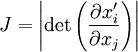
Or :
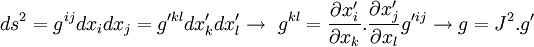
Donc :
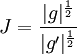
Ainsi
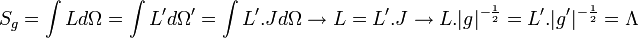
L'objectif est donc de trouver les scalaires du champ, invariants par rapport aux changements de référentiels.
En notant
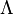
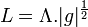
Définitions des tenseurs de Riemann, de Ricci, et de la courbure
À la manière d'Élie Cartan
En termes mathématiques, l'espace quadri-dimensionnel défini par les considérations ci-dessus est une variété C2 où les quadri-vitesses sont des vecteurs appartenant à l'espace vectoriel tangent au point où on a dérivé, cet espace vectoriel étant muni de la métrique
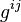
Rappelons que les coordonnées (x0;x1;x2;x3) sont les coordonnées des points de la variété, munie d'un système de coordonnées quelconque, représentant le choix arbitraire du référentiel physique de l'observateur.
La mesure de la gravitation, qui influe sur les géodésiques, peut se faire à travers la différence d'orientation entre deux vecteurs résultant du transport d'un seul vecteur d'origine par deux chemins géodésiques différents vers un même point final.
- L'équation des géodésiques
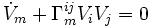
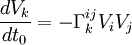
- Du fait que
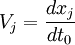
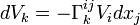
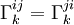
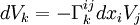
- De manière similaire, on obtient
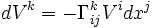
- Un vecteur
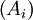
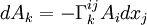
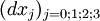
- À partir d'un point M quelconque de la variété, considérons deux variations infinitésimales
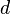
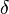
- 1er trajet :
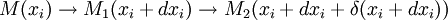
- 2ème trajet :
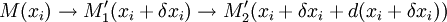
- Afin que ces deux trajets aboutissent au même point, on suppose que
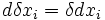
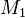
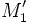
- Étudions les variations des coordonnées d'un vecteur
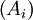
- 1er trajet :
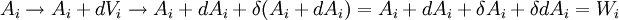
- 2ème trajet :
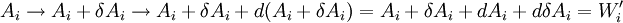
- On a :
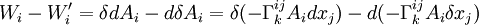
- Après quelques calculs, on obtient :
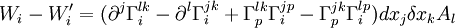
- On définit le tenseur de Riemann par :
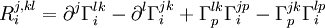
- L'égalité
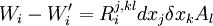
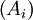
- On définit le tenseur de Riemann par :
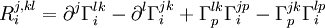
- Le tenseur de Ricci est une contraction du tenseur de Riemann :
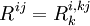
- Sa formule montre que c'est un tenseur symétrique :
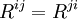
- La courbure riemannienne est le nombre obtenu par contraction du tenseur de Ricci :
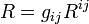
- Toutes les égalités utilisées dans « détails de la méthode d'Élie Cartan » étant indépendantes du référentiel choisi, et c'est aussi le cas pour les définitions des tenseurs de Riemann et de Ricci (c'est d'ailleurs pourquoi on se permet de les nommer tenseur ). C'est aussi le cas de la courbure
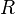
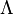
- Élie Cartan a démontré que les scalaires invariants par changement de référentiel sont de la forme
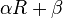
-
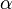
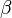
Outils analytiques
Une application du principe d'inertie dans l'espace courbe
Pour que notre travail soit bien une conséquence du principe de moindre action, la méthode utilisée ici consiste à déterminer les propriétés de la variété à partir de la métrique de ses espaces tangents.
- Les espaces vectoriels tangents (de dimension 4) sont munis de leur base « naturelle » {
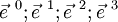
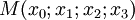
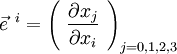
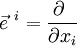
- Les équations des géodésiques sont des propriétés concernant les coordonnées
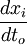
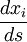
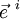
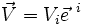
- Pour cela, nous pouvons utiliser un principe physique réécrit sur mesure pour la relativité générale :
- Principe d'inertie : le long d'une géodésique, et en l'absence d'intervention extérieure, le (quadri-)vecteur vitesse d'une particule est constant.
- C'est-à-dire :
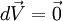
- On en tire :
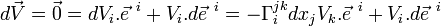
- Le quadri-vecteur vitesse initial étant quelconque, on obtient :
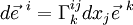
- En analysant les équations des géodésiques ou en tenant compte du fait que les « axes » des coordonnées ne sont pas obligatoirement des géodésiques, on ne peut pas affirmer que les coordonnées du quadri-vecteur vitesse sont constantes.
- Dériver signifie « déterminer la droite qui indique la direction du mouvement ». Tout le problème est de savoir ce qu'est une droite quand le système de coordonnées est quelconque, voire dans un espace courbe ; une fois les droites déterminées, la dérivation peut être définie.
- Dans le cadre qui nous intéresse, quand l'expérimentateur est dans un espace de Minkowski et qu'il a choisi un système de coordonnées quelconque, ce qui y induit éventuellement une gravitation, les droites de la dérivation sont celles de l'espace de Minkowski, qui sont aussi celles du mouvement inertiel. À moins de définir une nouvelle dérivation, l'égalité
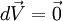
- Quand l'expérimentateur est dans un référentiel où il y a de la gravitation, et en l'absence d'information sur les causes de cette gravitation (due à une masse ou due à un référentiel accéléré, ou les deux) les seules droites auxquelles il a accès, en tant que physicien, sont celles du mouvement inertiel : la dérivation est donc définie par
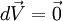
- Mais ce choix est basé sur l'hypothèse que, dans son référentiel, le mouvement inertiel suit bien une droite. Si l'expérimentateur choisit comme droites les axes de son référentiel, il impose donc
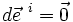
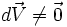
- Ces deux choix, comme d'autres que l'on peut imaginer, ne sont valables que localement :Le premier assimile localement la gravitation à un référentiel accéléré dans un espace de Minkowski, le deuxième émet l'hypothèse d'une force dans un espace initialement droit ; deux choix qui redressent à leur manière l'espace-temps, ce qui ne peut se faire que localement.
La dérivée covariante
Soit
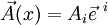
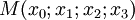
On a :
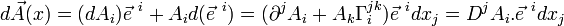
En définissant la dérivée covariante par :
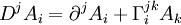
Propriété :
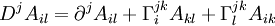
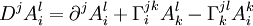
Et ainsi de suite avec tous les indices d'un tenseur, suivant leurs positions.
Où l'on retrouve les tenseurs de Riemann, etc.
À l'aide de la dérivée covariante, et après quelques calculs, on trouve :
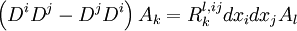
On obtient donc les notions déjà introduites « à la manière d'Élie Cartan ».
Égalités et propriétés utiles
- Théorème de Ricci :
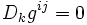
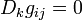
- En posant
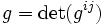
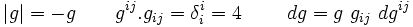
- Théorème d'Ostrogradski :
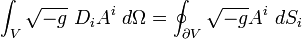
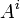
- La somme, la différence et la sommation d'Einstein de tenseurs définis dans le même espace tangent donnent un tenseur ; par contre s'il s'agit de tenseurs définis dans des espaces tangents différents, il n'est pas sûr que cela donne un tenseur.
- Par exemple : le symbole de Christoffel est défini à partir du tenseur métrique. L'équation des géodésiques
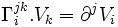
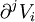
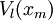
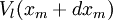
- Une égalité tensorielle démontrée en un point quelconque, mais en utilisant un référentiel particulier, est une égalité vraie en ce point et pour tous les référentiels : c'est là le principal intérêt d'utiliser des tenseurs.
- Par exemple, en tout point il existe un référentiel en apesanteur (en chute libre dans le champ de pesanteur), c'est-à-dire pour lequel
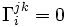
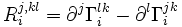
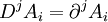
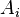
Les équations d'Einstein du champ de gravitation dans le cas extérieur
Les tenseurs sont utilisés pour s'assurer que les égalités sont vraies quel que soit le point d'observation du physicien et quel que soit son référentiel. Les tenseurs ne transportent que des informations liées au point d'observation et à son espace tangent, du coup, les informations qui y sont utilisées et qui en sont produites ne sont que locales : ce sont des informations sur les tenseurs, mis à part les données universellement valables comme les constante c, G, et autres que l'on pourra y trouver.
Le premier cas des équations du champ est le cas où il n'y a pas de matière (localement) : on parle du « cas extérieur », sous entendu « à la matière ».
Dans ce cas, la seule composante de l'action est la composante du champ gravitationnel
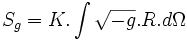
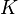
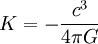

Pour trouver les équations du champ de gravitation sous la forme de tenseurs de densité d'énergie qui soient symétriques, il est plus simple de transformer le lagrangien sous l'intégrale de l'action que d'utiliser les équations d'Euler-Lagrange. Le principe variationnel est appliqué en faisant varier les termes de la métrique
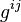
En utilisant l'égalité
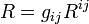
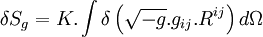
![= K [ \int \delta ( \sqrt{-g})g_{ij}R^{ij} d\Omega + \int \sqrt{-g}.\delta(g_{ij}).R^{ij} d\Omega + \int \sqrt{-g}.g_{ij}.\delta(R^{ij}) d\Omega ]](https://static.techno-science.net/illustration/Definitions/autres/9/989ccb9d5d9a98ff1ce8cbfe3f2f277f_d9020e41e3110a02cdca1e182dbeafc3.png)
On a
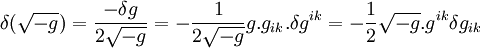
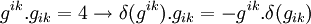
Pour la 1re intégrale, on a
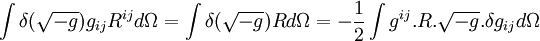
La 2e égalité est laissée inchangée.
Pour la 3e intégrale, pour simplifier les calculs, on se place dans un référentiel en apesanteur et on a donc
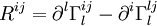
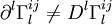
D'où
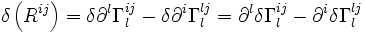
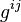
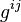
Dans n'importe quel référentiel,
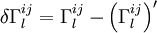
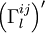
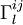
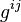
on a
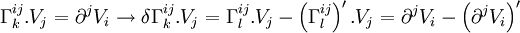
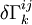
Et pour ce tenseur, dans le référentiel en apesanteur (et laissé comme tel, au point considéré, par la variation des
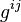
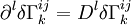
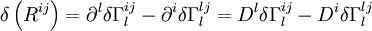
![\sqrt{-g}.g_{ij}.\delta R^{ij} = \sqrt{-g}.[g_{ij}.D^l \delta\Gamma_l^{ij} - g_{ij}.D^i \delta\Gamma_l^{lj}] = \sqrt{-g}.[D^l \left( g_{ij}.\delta\Gamma_l^{ij} \right) - D^i \left( g_{ij}.\delta\Gamma_l^{lj} \right) ]](https://static.techno-science.net/illustration/Definitions/autres/d/da0cdab8aabb5228e2ea17a1a4bb2abc_68946f8e8300462b59e96d8f0df73617.png)
car
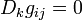
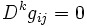
d'où
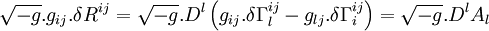
D'où, en utilisant le théorème d'Ostrogradski,
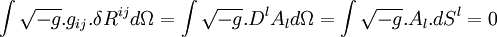
La nullité de la dernière intégrale est due au fait qu'elle est calculée sur l'hypersurface délimitant le volume d'intégration et au fait que les variations des
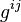
On obtient :
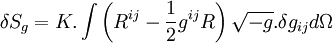
Le principe de moindre action disant que
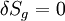
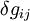
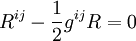
Les équations déduites sont :
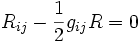
En faisant la « contraction »
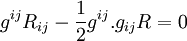
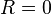
Les équations d'Einstein dans le cas extérieur sont donc :
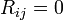
Les équations d'Einstein du champ de gravitation dans le cas intérieur
Le deuxième cas des équations du champ est le cas où il y a de la matière (localement) : on parle du « cas intérieur », c'est-à-dire « dans la matière ».
Dans ce cas, l'action est composée de l'action du champ gravitationnel
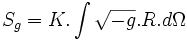
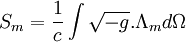
En utilisant la même méthode variationnelle, en sachant que
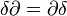
![\int \part_l [ \frac{\part \left( \sqrt{-g} \Lambda_m \right)}{\part \left( \part_l g_{ik} \right)} ] d \Omega = \int \part_l [ \sqrt{-g} \frac{\part \left( \Lambda_m \right)}{\part \left( \part_l g_{ik} \right)} ] d \Omega = \int \sqrt{-g} \frac{\part \left( \Lambda_m \right)}{\part \left( \part_l g_{ik} \right)} dS_l = 0](https://static.techno-science.net/illustration/Definitions/autres/6/674d7417b7e40778078b910f94a01f76_5abf1919bdbf42c889bc9b1c2f657fbd.png)
En définissant le tenseur impulsion-énergie
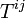
![\frac{1}{2} T^{ij} \sqrt{-g} = \frac{\part \left( \sqrt{-g} \Lambda_m \right)}{\part g_{ik}} - \part_l [ \frac{\part \left( \sqrt{-g} \Lambda_m \right)}{\part \left( \part_l g_{ik} \right)} ]](https://static.techno-science.net/illustration/Definitions/autres/1/1f33a12d59f9b9968327be856e7aad7d_a52c3af1fb2f66261a0ca549d9d2aa71.png)
On obtient :
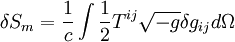
D'où, en posant
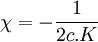
Les équations déduites sont :
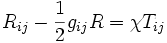
Avec la contraction similaire au cas extérieur, sachant que
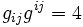
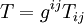
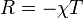
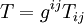
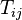
On peut donc aussi écrire :