Principe variationnel - Définition

Introduction

Un principe variationnel est un principe physique issu d'un problème exprimé sous une forme variationnelle. Dans de nombreux cas, la résolution des équations de la mécanique peut se ramener à la recherche de géodésiques dans un espace général approprié. D'une part, nous savons que ces géodésiques sont les extrémales d'une certaine intégrale représentant la longueur de l'arc joignant les points fixes dans cet espace. Par conséquent, nous pouvons déjà prévoir qu'au moins dans certains cas, les problèmes de mécanique pourront s'exprimer comme des problèmes aux variations, autrement dit, en postulant que la variation première d'une certaine intégrale est nulle. On dira qu'on a réduit les problèmes à leur forme variationnelle. D'autre part, les équations d'Euler établies en mathématiques pour un problème aux variations sont semblables aux équations de Lagrange établies en physique pour résoudre des problèmes de mécanique ; cette similitude suggère bien évidemment aussi la possibilité de cette réduction à une forme variationnelle.

Principe de Fermat

Bien qu'on puisse suivre la trace des principes variationnels d'une façon quasi continue de l'Antiquité à nos jours, il faut attendre plus d'un millénaire et demi — de Héron d'Alexandrie (vers la fin du I^er siècle ou le début du II^e siècle) au XVII^e siècle — jusqu'à Pierre de Fermat (1601–1665) pour en retrouver une application pratique. Le principe de Fermat, applicable aux rayons lumineux, peut s'écrire comme suit en tenant compte des perfectionnements intervenus depuis l'époque de Fermat lui-même :

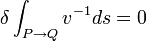
où P et Q sont deux points fixes, désigne la vitesse de phase de la lumière et ds est l'élément d'arc du trajet emprunté par le rayon lumineux et le symbole indique qu'il est fait une infime variation du trajet emprunté pour aller de P à Q.

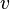
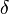
La vitesse de phase de la lumière, autrement dit sa vitesse de propagation, peut varier avec le point considéré, mais non avec la direction du rayon en ce point. Cette équation exprime que la variation (indiquée par la lettre grecque δ) de l'intégrale curviligne est nulle, c'est-à-dire que la différence entre cette intégrale évaluée le long de la trajectoire réelle et l'intégrale évaluée le long de n'importe quelle trajectoire virtuelle infiniment voisine est un infiniment petit du second ordre. Ceci ne signifie pas que l'intégrale est minimum, mais seulement qu'elle est extrémum. En effet, c'est seulement dans le cas où le trajet PQ est suffisamment petit, de manière à ce que des rayons « voisins » ne puissent recouper le rayon réel, que l'on peut démontrer qu'il s'agit effectivement d'un minimum.

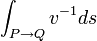
Seulement la propriété que la première variation est nulle peut être étendue à un trajet PQ arbitraire, d'où le nom moderne de « principe variationnel » plutôt que celui, ancien, de « principe de minimum ». Et il faut bien reconnaître que cette modification de terme et d'interprétation fait perdre au principe de Fermat, sinon de son utilité, au moins un peu de la valeur esthétique et philosophique qui a indéniablement joué un rôle dans son élaboration.

L'étude de certains systèmes optiques simples permet d'illustrer le problème. En effet, représentons le milieu hétérogène étudié par un de ces systèmes optiques. Dans cet exemple, l'image du point P, c'est-à-dire le lieu des points de rencontre de tous les rayons issus de P sous des angles légèrement différents, est constituée de deux focales EF et GH dont la distance caractérise l'astigmatisme du système. On peut alors montrer que l'intégrale curviligne est minimale si le second point considéré, à savoir Q, tombe avant les deux focales, qu'elle est maximale si Q tombe après les deux focales, et qu'elle satisfait à une condition mixte (elle n'est ni un minimum, ni un maximum) si Q tombe entre les deux focales.