Principe variationnel - Définition
La liste des auteurs de cet article est disponible ici.
Principe de Hamilton ou principe de moindre action de Lagrange
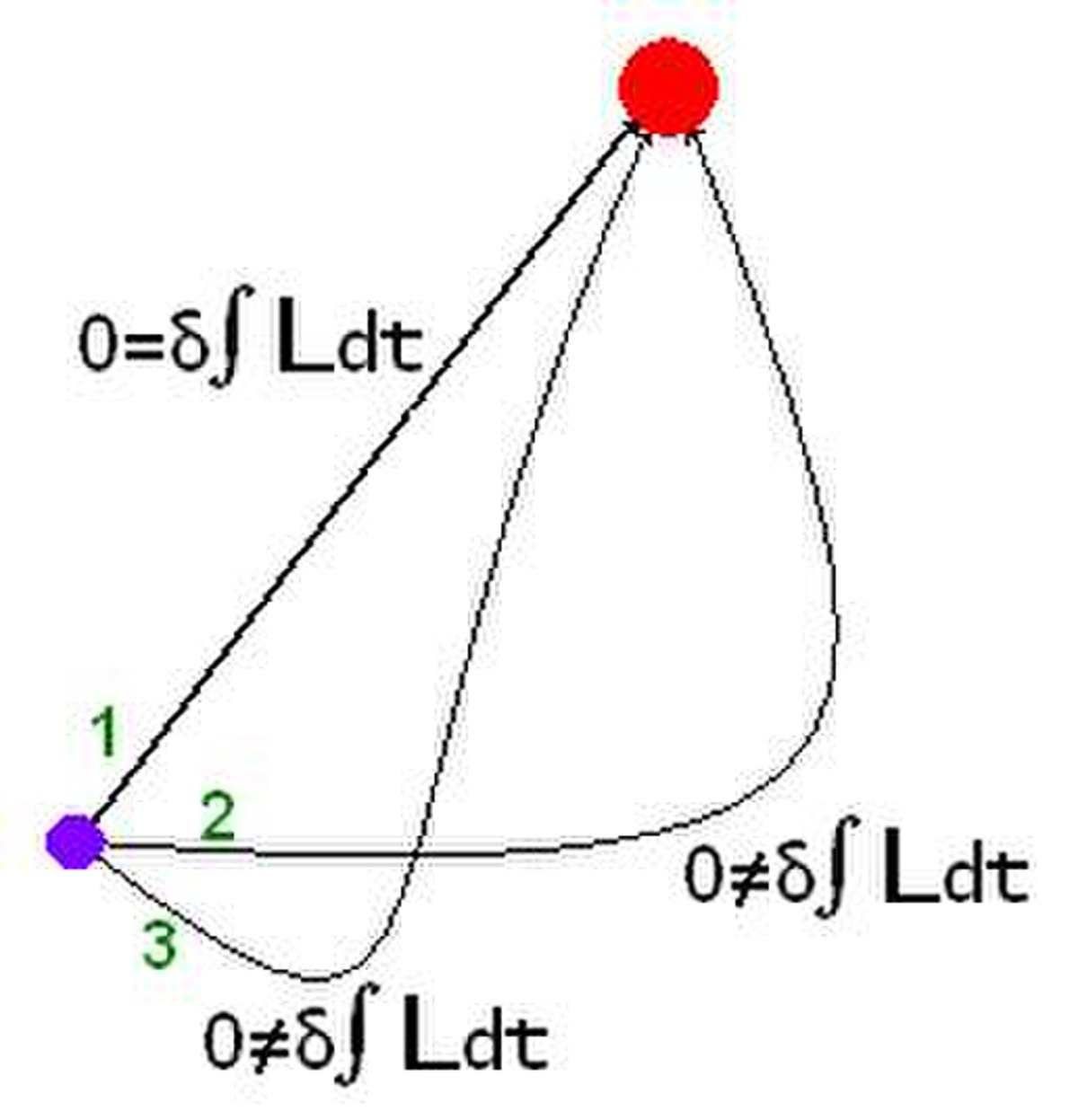
Si nous admettons que toutes les trajectoires variées passent par les mêmes extrémités Qo, Q1 au même instant to, t1 que la trajectoire réelle, la variation de l'intégrale d'action
![\delta \mathcal{S} = \delta \int_{t_0}^{t_1} \mathcal{L} dt = \int_{t_0}^{t_1} \sum_k \left[ \dfrac{ \partial \mathcal{L} }{ \partial q_k} - \dfrac{d}{dt}\left( \dfrac{\partial \mathcal{L}}{\partial \dot{q}_k} \right) \right] \delta^{'} q_k dt = 0](https://static.techno-science.net/illustration/Definitions/autres/a/a6f9bdf4032ef5053fc826290971e6b6_ab2201745a6dafb7a26b5aa2c7d7b49d.png)
d'après les équations de Lagrange. Inversement, si
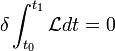
il faut que les équations de Lagrange soient satisfaites, puisque les δ'qk sont des quantités petites arbitraires. On peut encore en conclure que les équations d'Euler du problème aux variations sont identiques aux équations de Lagrange. Dès lors, le principe de Hamilton peut s'énoncer comme suit : Un système se meut d'une configuration à une autre de telle façon que la première variation de l'action
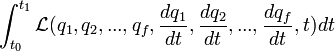
entre la trajectoire naturelle effectivement suivie et toute trajectoire virtuelle infiniment voisine ayant les mêmes extrémités dans l'espace et dans le temps soit nulle.
Ce principe possède une importance considérable qui dépasse l'équivalence formelle entre deux formulations mathématiques équivalentes du même problème. Ceci a d'ailleurs aussi son intérêt : par exemple, cette forme reste évidemment vraie dans n'importe quel système de coordonnées et, partant, on peut en déduire immédiatement l'invariance des équations de Lagrange pour toute transformation de coordonnées
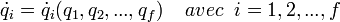
Mais surtout, ce principe ouvre la voie à une description de systèmes non-mécaniques par les méthodes mathématiques de la mécanique classique, comme dans la théorie des champs.
Fonction de Hamilton ou Hamiltonien
Le principe de Fermat est un principe variationnel particulièrement utile à l'optique géométrique. Pour résoudre des problèmes de mécanique, on utilise des principes variationnels faisant intervenir la fonction de Hamilton, que l'on désigne le plus souvent sous le terme de « Hamiltonien ». Pour arriver à comprendre le sens de cette fonction, considérons un problème à liaisons holonomes mais pouvant dépendre du temps t et qui admet le Lagrangien
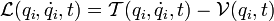
et étudions la valeur que prend l' intégrale d'action
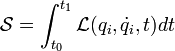
au cours de l'évolution du système mécanique considéré.
Supposons qu'au cours du mouvement naturel du système, le point représentatif dans l'espace de configuration parte d'une position initiale Q0 à l'instant t0 pour aboutir au point Q1 à l'instant t1. Cette trajectoire naturelle est représentée schématiquement sur la figure ci-contre par la courbe en rouge. Considérons un mouvement arbitraire partant de Po voisin de Qo à l'instant to + δto pour aboutir au point P1 voisin de Q1 à l'instant t1 + δt1.
Nous désirons comparer les valeurs de
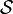
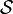
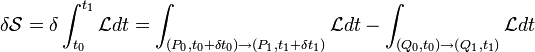
Au point M de coordonnées (q1,q2,...,qf), atteint sur la trajectoire naturelle à l'instant t, nous associerons sur la trajectoire virtuelle arbitraire le point M' de coordonnées (q1+δ'q1,q2+δ'q2,...,qf+δ'qf) atteint également au même instant t. Soit Q'o le point de la trajectoire variée, c'est–à-dire infiniment voisine de la trajectoire naturelle, atteint à l'instant to, et soit Q'1 celui qui correspond à l'instant t1. Notons les composantes de QoPo, QoQ'o, Q'oPo par δqi,o, δ'qi,o, Δqi,o = (dqi,o/dt) δto, respectivement, et celles de Q1P1, Q1Q'1, Q'1P1 par δqi,1, δ'qi,1, Δqi,1 = q'i,1 δt1, respectivement.
La vitesse q'i,1 sur la trajectoire variée ne diffère de celle sur la trajectoire réelle que par une quantité infiniment petite, laquelle ne donnerait dans Δqi,1 qu'une correction du second ordre. En séparant les intégrations sur les segments terminaux Q'oPo et P1Q'1, nous obtenons :
![\delta \mathcal{S} = [ \mathcal{L}_1 \delta t_1 ]_{Q^{'}_1 P_1} - [ \mathcal{L}_0 \delta t_0 ]_{Q_0^{'} P_0} + \int_{ (Q_0^{'}, t_0) \rightarrow ( Q_1^{'}, t_1)} \mathcal{L} dt - \int_{ (Q_0, t_0) \rightarrow ( Q_1, t_1)} \mathcal{L} dt = [\mathcal{L}_1 \delta t_1]_{Q^{'}_1 P_1} - [ \mathcal{L}_0 \delta t_0 ]_{Q_0^{'} P_0} + \int_{ t_0 }^{t_1} \delta^{'} \mathcal{L} dt \;\;\;\;\; (1)](https://static.techno-science.net/illustration/Definitions/autres/6/6f1f2bdc0a127b3da79e00c0d5da98f9_f0b305b9d1304e9ba89f8da06531350a.png)
L'intégrand δ'L dans la dernière intégrale est calculé entre des points des deux trajectoires correspondant aux mêmes instants t. On trouve que l'intégrale ∫to→t1 δ'L dt vaut
![\int_{t_0}^{t_1} \delta^{'} \mathcal{L} dt = \sum_k \left[ \dfrac{ \partial \mathcal{L}}{\partial \dot{q}_k} \delta^{'} q_k \right]_1 - \sum_k \left[ \dfrac{ \partial \mathcal{L}}{\partial \dot{q}_k} \delta^{'} q_k \right]_0 + \int_{t_0}^{t_1} \sum_k \left[ \dfrac{ \partial \mathcal{L}}{\partial q_k} - \dfrac{d}{dt} \left( \dfrac{ \partial \mathcal{L}}{\partial \dot{q}_k}\right) \right] \delta^{'} q_k dt \;\;\;\;\; (2)](https://static.techno-science.net/illustration/Definitions/autres/e/e1f9abb920e37ffb703e838a66c8a7b0_c8284cca314a417cc0b8e153522b5887.png)
En introduisant les moments conjugués pk aux coordonnées généralisées contravariantes qk, qui représentent les composantes covariantes de la vitesse, et en se souvenant que selon les équations de Lagrange, l'expression figurant entre crochets dans le dernier terme est nulle, on trouve finalement
![\delta \mathcal{S} = [ \mathcal{L}_1 \delta t_1 ]_{Q^{'}_1 P_1} - [ \mathcal{L}_0 \delta t_0 ]_{Q_0^{'} P_0} + \int_{ (Q_0^{'}, t_0) \rightarrow ( Q_1^{'}, t_1)} \mathcal{L} dt + \sum_k p_{k,1} \delta^{'} q_{k,1} - \sum_k p_{k,0} \delta^{'} q_{k,0} \;\;\;\;(3)](https://static.techno-science.net/illustration/Definitions/autres/f/ff0659cfa87c57ba942729e91538948b_6b6f48c2b25d2faa9cc5c2dff5184788.png)
Comme δ'q1 = Q1Q'1 = Q1P'1 – Q'1P'1, il vient en termes de composantes : δ'qk1 = δqk1 – Δqk1 = δqk1 – q'k1 δt1 et de même δ'qko = δqko – Δqko = δqko – q'ko δto. Dès lors, utilisant ces relations, on trouve sous forme condensée
![\delta \mathcal{S} = \left[ \sum_k p_k \delta q_k - \mathcal{H} \delta t \right]_0^1](https://static.techno-science.net/illustration/Definitions/autres/3/3c6210de6e1fd153596192c103c4cc7a_5af50c590f3306627982fc489a64a9ea.png)
en définissant la fonction de Hamilton (ou le Hamiltonien)
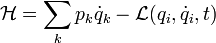
La fonction de Hamilton joue un rôle essentiel dans les principes généraux de la mécanique.