Programmation linéaire - Définition

Programmation linéaire en nombres entiers

Un problème de programmation linéaire en nombres entiers (PLNE) n'est pas un programme linéaire dans le sens où son domaine de réalisabilité n'est pas un polyèdre mais un ensemble discret de points. Pourtant, on peut le décrire comme un PL auquel on ajoute la contrainte supplémentaire que certaines variables ne peuvent prendre que des valeurs entières. On distingue le programme linéaire mixte avec variables entières et continues du programme entier avec toutes ses variables entières.

La PLNE est un problème NP-complet car de nombreux problèmes NP-complets peuvent être exprimés comme des PLNE (par exemple trouver un stable dans un graphe G = (V,E) revient à trouver un vecteur satisfaisant pour tout arête ). Les algorithmes décrits ci-dessus pour la PL ne résolvent pas les problèmes de PLNE. Algorithmiquement donc, la résolution d'un PLNE est autrement plus difficile celle d'un PL qui joue pourtant un rôle crucial quant à leur résolution, principalement pour deux raisons. Premièrement, la relaxation continue d'un PLNE (c'est le PLNE sans les contraintes d'intégrité) est un PL qui peut être résolu efficacement et fournir ainsi une borne duale (dans le sens non-réalisable). Les algorithmes de résolution de PLNE, tels que les algorithmes par séparation et évaluation se basent sur cette relaxation continue pour diminuer au maximum l'énumération des solutions. Deuxièmement, le théorème Optimisation/Séparation de Grötschel, Lovasz et Schrijver permet de résoudre en pratique par la PL les problèmes entiers dont on connait une bonne description polyèdrale (c'est-à-dire dont on peut séparer les contraintes en temps polynomial). C'est le principe de fonctionnement des algorithmes de plans sécants.

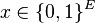
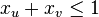
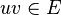
Algorithmes de la programmation linéaire

L'algorithme du simplexe permet de résoudre les problèmes de PL en construisant tout d'abord une solution réalisable qui est un sommet du polytope puis en se déplaçant selon les arêtes du polytope pour atteindre des sommets pour lesquels la valeur de l'objectif est de plus en plus grande, jusqu'à atteindre l'optimum. Bien que cet algorithme soit efficace en pratique et qu'il soit assuré de trouver l'optimum, son comportement dans le pire cas peut être mauvais. Il est ainsi possible de construire un PL pour lequel la méthode du simplexe requiert un nombre d'étapes exponentiel en la taille du problème. Ainsi, pendant plusieurs années, savoir si la PL était un problème NP-complet ou polynomial est resté une question ouverte.

Le premier algorithme polynomial pour la PL a été proposé par Leonid Khachiyan en 1979. Il est basé sur la méthode de l'ellipsoïde en optimisation non linéaire précédemment proposée par Naum Shor. Cette méthode est elle-même une généralisation de la méthode de l'ellipsoïde en optimisation convexe due à Arkadi Nemirovski (Prix John von Neumann 2003), et à David B. Yudin.

Cependant, l'efficacité pratique de l'algorithme de Khachiyan est décevante : l'algorithme du simplexe est pratiquement toujours plus performant. En revanche, ce résultat a encouragé la recherche dans les méthodes de point intérieur. Par opposition à l'algorithme du simplexe qui considère uniquement la frontière du polytope définie par les contraintes, les méthodes de point intérieur évoluent à l'intérieur du polytope.

En 1984, N. Karmarkar propose la méthode projective. C'est le premier algorithme efficace à la fois en théorie et en pratique. Sa complexité dans le pire cas est polynomiale et les expérimentations sur les problèmes pratiques montrent que la méthode peut raisonnablement être comparée à l'algorithme du simplexe. Depuis lors, plusieurs méthodes de point intérieur ont été proposées et étudiées. Une des méthodes les plus célèbres est la méthode prédictive/corrective qui fonctionne très bien en pratique même si son étude théorique est encore imparfaite.

Implémentations en pratique

Pour la résolution pratique de problèmes de PL ordinaires, il est commun de considérer comme équivalents les (bons) codes basés sur les méthodes dérivées du simplexe ou du point intérieur. De plus, pour la résolution de problèmes de grande taille, une technique comme la génération de colonnes peut se révéler extrêmement efficace.

Les solveurs basés sur la PL sont de plus en plus utilisés pour l'optimisation de divers problèmes industriels tels que l'optimisation des flux de transports ou la planification de la production. Toutefois, les modèles de PL se révèlent insuffisants pour représenter de nombreux problèmes. Une extension possible est alors la programmation linéaire en nombres entiers (PLNE), qui permet de modéliser un grand nombre de problèmes supplémentaires, notamment les problèmes NP-complets.

On retrouve des solveurs de PL dans de nombreux outils comme MATLAB, SAGE ou Excel.