Racine d'un nombre - Définition
La liste des auteurs de cet article est disponible ici.
Résolution par radicaux
Il a été une fois conjecturé que toutes les racines de polynômes pouvaient être exprimées en termes de radicaux et d'opérations élémentaires. Ceci n'est pas vrai en général comme l'énonce le théorème d'Abel-Ruffini. Par exemple, les solutions de l'équation
ne peuvent pas être exprimées en termes de radicaux.
Pour résoudre n'importe quelle équation de n-ième degré, voir l'algorithme de recherche de racines.
Racines d'un complexe
Pour tout entier naturel non nul n, une racine n-ième d'un nombre complexe z est un nombre, qui élevé à la puissance n donne z, c'est-à-dire une solution de l'équation
- xn = z
d'inconnue x.
Lorsque z est différent de 0, il existe n racines n-ièmes distinctes de z. En effet, les racines n-ièmes d'un complexe z non nul sont aussi les racines du polynôme Xn − z, qui admet bien n solutions dans l'ensemble des nombres complexes d'après le théorème de d'Alembert-Gauss.
Toutes les racines de n'importe quel nombre, réel ou complexe, peuvent être trouvées avec un simple algorithme. Le nombre doit d'abord être écrit sous la forme
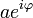
pour
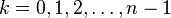
![\sqrt[n]{a}](https://static.techno-science.net/illustration/Definitions/autres/9/9a2b6d33f3d62a1e8bd99c76f3cb79f5_0c5fa6f789d712e9c11486377ac71201.png)
Nombres réels positifs
Toutes les solutions complexes de xn = a, autrement dit les racines n-ièmes de a, où a est un nombre réel positif, sont données par l'équation simplifiée :
pour
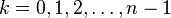
![\sqrt[n]{a}](https://static.techno-science.net/illustration/Definitions/autres/9/9a2b6d33f3d62a1e8bd99c76f3cb79f5_0c5fa6f789d712e9c11486377ac71201.png)
Racines de l'unité
Lorsque z = 1, une telle racine s'appelle une racine n-ième de l'unité, et l'ensemble des racines n-ièmes de l'unité, noté
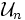
- Xn − 1.
Il s'agit d'un sous-groupe cyclique du groupe multiplicatif des complexes de module 1. Il est formé des éléments
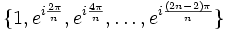
On appelle racine n-ième primitive de l'unité tout générateur du groupe cyclique
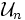
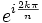
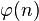

Racine en typographie
En typographie, une racine est composée de trois parties : le radical, l'indice et le radicande.
- Le radical est le symbole de la racine,
- l'indice est le degré de cette racine,
- enfin, le radicande est ce qu'il y a sous la racine.
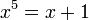
![e^{(\frac{\varphi+2k\pi}{n})i} \times \sqrt[n]{a}](https://static.techno-science.net/illustration/Definitions/autres/a/adb6eb95f204c635b43d16ebc4c65c31_cd1af837d1b6e1f2bdb43072edd02193.png)
![e^{2\pi i \frac{k}{n}} \times \sqrt[n]{a}](https://static.techno-science.net/illustration/Definitions/autres/f/fa1fa6c467c099ca972905f159336a24_43b58e7af388b105576eff5ebc9249e0.png)


















































