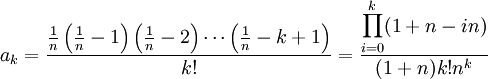Racine d'un nombre - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une racine n-ième d'un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul,
Selon que l'on travaille dans l'ensemble des réels positifs, l'ensemble des réels ou l'ensemble des complexes, le nombre de racines n-ièmes d'un nombre a peut être 0, 1, 2 ou n.
Pour un nombre réel a positif, il existe un unique réel b positif tel que bn = a. Ce réel est appelé la racine n-ième de a (ou racine n-ième principale de a ) et se note
![\sqrt[n]{a}](https://static.techno-science.net/illustration/Definitions/autres/9/9a2b6d33f3d62a1e8bd99c76f3cb79f5_0c5fa6f789d712e9c11486377ac71201.png)
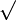
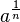
Le terme de racine d'un nombre ne doit pas être confondu avec celui de racine d'un polynôme qui désigne la (ou les) valeur(s) où le polynôme s'annule.
Racine d'un réel
Racine carrée
Pour tout réel r strictement positif, l'équation x2 = r admet deux solutions réelles opposées, et lorsque r = 0, l'équation x2 = 0 admet comme seule solution 0.
La racine carrée d'un réel r positif (
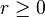
- x2 − r = 0 d'inconnue x.
Elle est notée
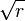
Exemples
- La racine carrée de deux est
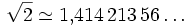
- La racine carrée de trois est
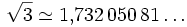
Racine cubique
La racine cubique d'un réel r quelconque est l'unique racine réelle de l'équation
- x3 − r = 0 d'inconnue x.
Elle est notée
![\sqrt[3]{r}](https://static.techno-science.net/illustration/Definitions/autres/d/d365666989b9eb9c410ae129d61495cd_b8844fcd06eb7b0c66f8e767f7daa6ac.png)
Exemple:
- On a
![\sqrt[3]{-8}=-2](https://static.techno-science.net/illustration/Definitions/autres/1/154ab22db729e6b6490caa36d8669830_2ec9db02a4410750766a6dc7dfb8fc19.png)
Racine n-ième d'un nombre réel positif
Pour tout entier naturel non nul n, l'application
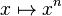
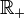
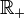
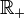
La racine énième (ou racine n-ième) d'un réel r positif (r ≥ 0, n > 0) est l'unique solution réelle positive de l'équation
- xn − r = 0 d'inconnue x.
Elle est notée
![\sqrt[n]{r}](https://static.techno-science.net/illustration/Definitions/autres/0/0c1dda2d990c60ca5ef80cd446e594db_ba05f1b176994ec109d16d310865c6b1.png)
Remarquons que la racine n-ième de r est aussi l'unique racine positive du polynôme Xn − r.
Lorsque n est pair, l'équation
- xn − r = 0 d'inconnue x
possède deux solutions qui sont
![\sqrt[n]{r}](https://static.techno-science.net/illustration/Definitions/autres/0/0c1dda2d990c60ca5ef80cd446e594db_ba05f1b176994ec109d16d310865c6b1.png)
![-\sqrt[n]{r}](https://static.techno-science.net/illustration/Definitions/autres/5/5ed035388b762db2a0eaeec7fcfa09d4_f08b6fd81234a5d7185b295347801cc2.png)
Lorsque n est impair, l'équation
- xn − r = 0 d'inconnue x
ne possède qu'une seule solution
![\sqrt[n]{r}](https://static.techno-science.net/illustration/Definitions/autres/0/0c1dda2d990c60ca5ef80cd446e594db_ba05f1b176994ec109d16d310865c6b1.png)
Racine n-ième d'un nombre réel négatif
Le traitement des racines de nombres négatifs n'est pas uniforme. Par exemple, il n'existe pas de racine carrée réelle de -1 puisque pour tout réel x, x2 + 1 > 0, mais la racine cubique de -27 existe et est égale à -3.
Pour tout entier naturel impair n, l'application
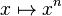


Pour tout entier naturel impair n, la racine énième (ou racine n-ième) d'un réel r quelconque est l'unique solution réelle de l'équation
- xn − r = 0
d'inconnue x.
Il s'ensuit que les racines d'ordres impairs de nombres réels négatifs sont négatives.
Remarquons que pour les entiers naturels impairs n et pour tout réel a, on a
-
![\sqrt[n]{-a} =-\sqrt[n]{a}](https://static.techno-science.net/illustration/Definitions/autres/9/9a37133c90c25c3868fc8ff3ae45f12b_2ada0a5653957e9f80c9c0d75c0fbde9.png)
Le besoin de travailler avec des racines de nombres négatifs a conduit à la mise en place des nombres complexes, mais il y a également dans le domaine des nombres complexes des restrictions pour les racines. Voir ci-dessous.
Les propriétés des racines
Les règles de calcul des racines qui découlent des propriétés des puissances.
Pour les nombres strictement positifs, a et b, on a les règles de calcul suivantes:
Dans le cas des nombres négatifs, ces règles de calcul ne pourront être appliquées que si m et n sont des nombres impairs. Dans le cas des nombres complexes, elles sont à éviter.
Exposant fractionnaire
Dans l'ensemble des réels strictement positifs, le nombre qui, élevé à la puissance n, donne a est noté
![\sqrt[n]{a}](https://static.techno-science.net/illustration/Definitions/autres/9/9a2b6d33f3d62a1e8bd99c76f3cb79f5_0c5fa6f789d712e9c11486377ac71201.png)
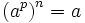
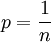
Ainsi on peut noter la racine carrée de a ,
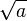
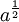
![\sqrt[3] a](https://static.techno-science.net/illustration/Definitions/autres/2/23c75e34f5a80b030b27191fe1762656_ff2bc432e72c3bfe557cfc3d5a492761.png)
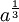
![\sqrt[n] a](https://static.techno-science.net/illustration/Definitions/autres/c/cd8ba43c413c424322b9b5ebb28ea659_74adab2e033e22413a537950f12cc309.png)
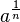
Cette extension des valeurs possibles pour l'exposant est due au travail de Newton et Leibniz. On peut poursuivre le travail en observant que
et vérifier que cette notation est compatible avec les propriétés déjà connues sur les exposants entiers.
C'est chez Newton que l'on voit apparaître pour la première fois un exposant fractionnaire. Mais Newton et Leibniz ne s'arrêteront pas là et se poseront même la question de travailler sur des exposants irrationnels sans être pour autant capables de leur donner un sens. Ce n'est qu'un siècle plus tard que ces notations prendront un sens précis avec la mise en place de la fonction exponentielle et la traduction :
-
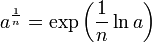
Fonction racine n-ième
Pour tout entier naturel non nul n, l'application
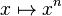
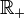
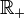
On remarque que cette fonction est continue sur l'intervalle
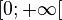
Les formules sur la dérivée de la réciproque permettent d'établir que la fonction racine n-ième est dérivable sur l'intervalle
![]0; + \infty[](https://static.techno-science.net/illustration/Definitions/autres/a/abe7a92275e0c5644d5bd5c819fa694e_7de8844c4d1d9aa7fac379e65356ed74.png)
![x \mapsto \frac{\sqrt[n] x}{nx}](https://static.techno-science.net/illustration/Definitions/autres/c/cb039e269bc982f64954de515f42aad5_c4ba410057b0096fe47d399991f2b46f.png)
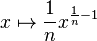
Développement en série entière
Le radical ou racine peut être représenté par la série :
où
avec | x | < 1.
![\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a \cdot b}](https://static.techno-science.net/illustration/Definitions/autres/7/73d577cd0a118df1dda404e72e4a922d_753269599b6f60e4c3b74a3aed8747d8.png)
![\sqrt[m]{\sqrt[n]{a}} = \sqrt[m \cdot n]{a}](https://static.techno-science.net/illustration/Definitions/autres/0/0a8209eed9a856af2b508dedfad9ffee_35b25850d30a6303cfa7fc0012505a58.png)
![\frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}](https://static.techno-science.net/illustration/Definitions/autres/8/81a910073a5639512945a6d1e8e0d102_9059ad0f99b033387afd783817d5d98b.png)
![\left(\sqrt[n]{a} \right)^m = \sqrt[n]{a^m}](https://static.techno-science.net/illustration/Definitions/autres/a/a852c0aa9734b397b1bd4b3a122b7f11_8b1c497e33b15fcb127fcb7413762168.png)
![\sqrt[n]{a^m} = \left(\sqrt[n] a\right)^m= \left(a^m\right)^{\frac 1n}= \left(a^{\frac 1n}\right)^m = a^{\frac mn}.](https://static.techno-science.net/illustration/Definitions/autres/3/371cf22e5fdbf65109b9cbfec4a803fc_3c863e05c1da35c764f5452b8dda59af.png)
![\sqrt[n]{1+x}=(1+x)^{\frac 1n} = \sum_{k=0}^\infty a_k x^k](https://static.techno-science.net/illustration/Definitions/autres/8/8086a9e4574f3d8fb9824ae01e4955c9_9c2abb627bf4330973811877d3fc8c26.png)