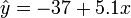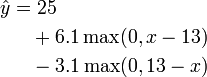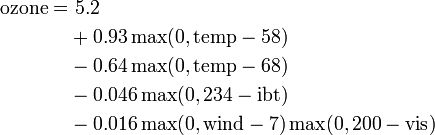Régression multivariée par spline adaptative - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La Régression multivariée par spline adaptative (en anglais MARS pour « Multivariate adaptive regression splines ») est une forme de modèle de régression présentée pour la première fois par Jerome H. Friedman et Bernard Silverman en 1991. C'est une technique de régression non paramétrique qui peut être vue comme un extension des modèles linéaires qui modèle automatiquement des interactions et des non-linéarités. Le terme MARS est une marque de Salford Systems.
Introduction
Soit une matrice de variables d'entrées x, et un vecteur de réponses observées y avec une réponse pour chaque ligne de x. Par exemple :
| x | y |
|---|---|
| 10.5 | 16.4 |
| 10.7 | 18.8 |
| 10.8 | 19.7 |
| ... | ... |
| 20.6 | 77.0 |
Ici il y a une seule Variable indépendante, aussi la matrice x est réduite a une seule colonne. Un Modèle linéaire pour les données ci-dessus serait :
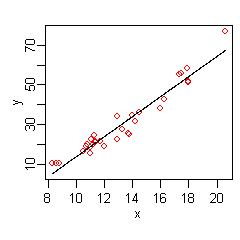
où
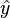
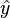
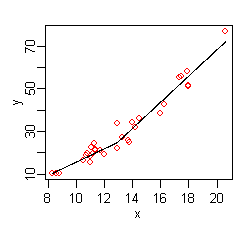
La figure à droite montre une estimation
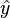
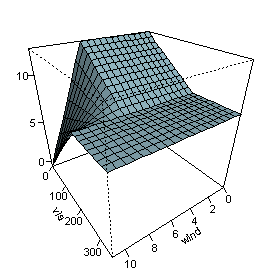
Cette expression modélise la pollution de l'air (niveau de l'ozone dans l'air) zn fonction de la température et de quelques autres variables. On peut remarquer que la dernière expression fait intervenir une interaction entre wind et vis. La figure sur la droite montre ozone lorsque wind et vis ( vent et force) varient, alors que les autres variables sont fixées à leur valeur médiane. La figure montre donc que le vent n'affecte pas le niveau de l'ozone dans l'air sauf si la visibilité est basse.
Logiciels
Libres
- Plusieurs packages R modélisent la Régression multivariée par spline adaptative:
- La fonction
polymarsdans le package polspline - La fonction
marsdans le package mda - La fonction
earthdans le package earth
- La fonction
- On trouve aussi MARS dans Matlab
Commerciaux
- MARS de Salford Systems
- STATISTICA de StatSoft
Modèle MARS
MARS construit des models de la forme
-
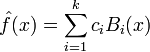
Le modèle est une somme pondérée de fonctions de bases Bi(x). Chaque ci étant un coefficient constant. Chaque fonction de base peut prendre l'une des trois formes suivantes :
- Une constante 1.
Il n'y a qu'un seul terme de ce type : l'intersection avec l'axe (la valeur moyenne de la variable à expliquer quand la variable explicative prend la valeur zéro). Dans l'exemple ici cette valeur est 5.2
- Une fonction charnière
- Un produit de fonctions charnières