Sous-ensemble - Définition

Théorie axiomatique des ensembles

En théorie des ensembles, dans la théorie des ensembles de Zermelo ou de Zermelo-Fraenkel, l'inclusion n'est pas une notion primitive. elle est définie à partir de l'appartenance comme indiquée au début de l'article. Comme déjà mentionné, des propriétés de l'inclusion, comme la réflexivité et la transitivité, sont des conséquences purement logique de cette définition et l'antisymétrie de l'inclusion est exactement l'axiome d'extensionnalité. L'existence d'un plus petit élément (ensemble vide) se montre par compréhension (voir axiome de l'ensemble vide). Il n'y a pas de plus grand élément pour l'inclusion dans l'univers de la théorie des ensembles : un ensemble qui contiendrait tous les ensembles (au sens de l'inclusion) serait, par l'axiome de la paire (cas du singleton), l'ensemble de tous les ensembles et l'on pourrait, en utilisant le schéma d'axiomes de compréhension, dériver le paradoxe de Russell. L'existence d'une borne inférieure (intersection) se démontre par compréhension. L'existence d'une borne supérieure (réunion), nécessite un axiome spécifique, l'axiome de la réunion. À chaque fois l'axiome d'extensionnalité est utile pour démontrer l'unicité.

L’existence de l'ensemble des parties d'un ensemble nécessite également un axiome spécifique, l’axiome de l'ensemble des parties, et son unicité est encore une fois assurée par l’axiome d'extensionnalité.

L'appartenance et l'inclusion sont en général bien distinctes dans les mathématiques ordinaires. En théorie des ensembles une notion très utile est celle d'ensemble transitif : un ensemble dont tous les éléments sont aussi des sous-ensembles ! En particulier Les ordinaux sont des ensembles transitifs. La restriction de l'inclusion à un ordinal définit un bon ordre (et donc un ordre total), l'ordre strict correspondant est l'appartenance.

Si on introduit, informellement ou non, la notion de classe (voir l'article correspondant), comme celle-ci correspond à la notion de prédicat, on peut définir de façon analogue l'inclusion entre classes. La classe de tous les ensembles est maximale pour l'inclusion. On peut définir l'intersection et la réunion de deux classes, et donc d'un nombre fini de classes par conjonction et disjonction, le passage au complémentaire, par négation. Le complémentaire d'un ensemble dans une classe propre, en particulier dans la classe de tous les ensembles, ne peut cependant être un ensemble (par réunion). Il n'est pas question par contre non plus d'ensemble, ou même de classe, des parties d'une classe propre.

Propriétés de l'inclusion

L'ensemble vide est l'ensemble qui n'a pas d'éléments, et on le note Ø.

Proposition (ensemble vide). L'ensemble vide est sous-ensemble de tout ensemble, c'est-à-dire que pour tout ensemble A :

∅ ⊂ A

Démonstration : nous devons démontrer que Ø est un sous-ensemble de A, c'est-à-dire que tous les éléments de Ø sont des éléments de A, mais il n’existe pas d’éléments de Ø. Pour qui a un peu la pratique des mathématiques, l' inférence « Ø n’a pas d’éléments, donc tous les éléments de Ø sont des éléments de A » est évidente, mais cela peut être dérangeant pour le débutant. Il peut être utile de raisonner différemment (par l’absurde). Si nous avions supposé que Ø n' était pas un sous-ensemble de A, nous aurions pu trouver un élément de Ø n’appartenant pas à A. Comme il n’existe pas d’élément de Ø, c’est impossible et donc Ø est par conséquent un sous-ensemble de A.

Nous avons aussi la proposition suivante.

Proposition (réflexivité). Tout ensemble est inclus dans lui-même, c'est-à-dire que pour tout ensemble A :

A ⊂ A.

On dit que l'inclusion est une relation réflexive. Pour le prouver, il suffit de reprendre la définition de l’inclusion.

Une autre propriété qui elle aussi repose seulement sur la définition de l'inclusion est la transitivité.

Proposition (transitivité). Pour trois ensembles quelconques A, B et C, si A est un sous-ensemble de B et B est un sous-ensemble de C, alors A est un sous-ensemble de C, c'est-à-dire que :

(A ⊂ B et B ⊂ C) ⇒ A ⊂ C.

Contrairement aux propositions précédentes, qui se démontrent de façon purement logique, en revenant aux définitions, la propriété d'antisymétrie repose sur la notion même d'ensemble : c'est en fait la simple traduction d'une propriété fondamentale des ensembles, dite propriété d'extensionnalité, à savoir que deux ensembles sont égaux si et seulement s'ils ont les mêmes éléments.

Proposition (antisymétrie). Deux ensembles A et B sont égaux si et seulement si A est un sous-ensemble de B et B est un sous-ensemble de A, c'est-à-dire :

A = B   si et seulement si   (A ⊂ B et B ⊂ A)

Quel que soit l’ensemble E, l’inclusion munit donc son ensemble des parties (E) d’une relation d'ordre, qui est un ordre partiel dès que E possède au moins deux éléments. En effet si a et b sont deux éléments distincts de E, les singletons {a} et {b} sont des parties de E qui ne se comparent pas pour l'inclusion. Cet ordre a toujours un plus petit élément, Ø l'ensemble vide, et un plus grand élément, l'ensemble E.

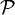
Cet ordre n'est donc pas total en général mais a d'autres propriétés remarquables.

Proposition (intersection finie). Pour deux ensembles A et B quelconques, on peut définir l'intersection de A et B, qui est l'ensemble des éléments communs à A et à B, noté A ∩ B. Cet ensemble est le seul à être inclus dans A et dans B, et à contenir tout ensemble contenu à la fois dans A et dans B :

A ∩ B ⊂ A    et    A ∩ B ⊂ B ;

si C ⊂ A et C ⊂ B, alors C ⊂ A ∩ B.

On dit que l'ensemble A ∩ B est la borne inférieure de A et B pour l'inclusion.

On a une propriété analogue (on dit duale, en un sens précis) pour la réunion.

Proposition (réunion finie). Pour deux ensembles A et B quelconques, on peut définir la réunion de A et B, qui est l'ensemble des éléments appartenant à A ou à B, noté A ∪ B. Cet ensemble est le seul à contenir à la fois A et B, et à être contenu dans tout ensemble contenant à la fois A et B :

A ⊂ A ∪ B    et    B ⊂ A ∪ B ;

si A ⊂ C et B ⊂ C, alors A ∪ B ⊂ C.

On dit que A ∪ B est la borne supérieure de A et B pour l'inclusion.

Pour tout ensemble E l'inclusion munit donc (E) d'une structure d'ordre que l'on appelle un treillis. On peut définir l'inclusion à partir de l'intersection ou de la réunion (c'est une propriété commune aux treillis) :

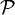
A ⊂ B   si et seulement si   A ∩ B = A ;

A ⊂ B   si et seulement si   A ∪ B = B.

Du fait des propriétés de distributivité de la réunion vis-à-vis de l'intersection, et de l'intersection vis-à-vis de la réunion, ce treillis est dit distributif.

Des propriétés des intersections et réunions binaires, on pourrait déduire facilement un résultat analogue pour les intersections et réunions finies, mais on a un résultat plus fort :

Proposition (intersection et réunion quelconques). Pour une famille quelconque d'ensembles (A_i)_{i ∈ I}, on peut définir l'intersection des éléments de la famille, ∩_{i ∈ I}A_i, et leur réunion ∪_{i ∈ I}A_i. L'intersection des A_i est le plus grand des ensembles inclus dans chacun des A_i, la réunion des A_i est le plus petit des ensembles incluant tous les A_i.

Le treillis de l'inclusion sur (E) est dit complet. Il s'agit même d'une algèbre de Boole, puisque tout sous-ensemble de E a un complémentaire dans E.

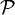
Proposition (complémentaire). Soit E un ensemble. On appellera complémentaire d'un sous-ensemble A de E, le sous-ensemble de E constitué des éléments de E qui ne sont pas dans A, et on le notera A^c. On a :

A ∩ A^c = ∅   et   A ∪ A^c = E

On montre alors que :

A ⊂ B   si et seulement si    B^c ⊂ A^c