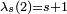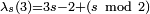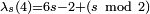Suite de Davenport-Schinzel - Définition

Limites aux longueurs

La complexité des suites DS(n,s) a été analysée asymptotiquement lorsque n tend vers l'infini, en supposant que s est une constante fixe. Des bornes fortes presque optimales sont connues pour tout s.

Soit λ_s(n) la longueur de la suite DS(n,s) la plus longue. Les meilleurs limites connues sur λ_s utilisent la fonction d'Ackermann inverse.

α(n) = min { m | A(m,m) ≥ n },

où A est la fonction d'Ackermann. En raison de la croissance très rapide de la fonction d'Ackermann, son inverse α croît très lentement, et est d'au plus quatre pour les problèmes de taille pratique.

Avec les notations de Landau (o et O), on connait les limites suivantes :

• λ₁(n) = n,
• λ₂(n) = 2n − 1.
• . Cette borne de complexité peut être réalisée avec un facteur constant par des segments de droite : il existe des arrangement de n segments de droite dans le plan dont les enveloppes les plus basses ont la complexité Ω(n α(n)).
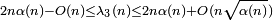
• pour les valeurs paires de s≥ 4, , où t = s/2 − 1.
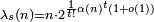
• pour les valeurs impaires de s≥ 5, .

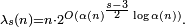
La valeur de λ_s(n) est connue également lorsque s est variable et n une constante petite :