Surya Siddhanta - Définition

Application au calendrier

Almanach hindou pour l'année 1871-1872

Dans les différentes régions de l’Inde, on utilise largement les calendriers solaire et calendrier luni-solaires indiens avec leurs variantes locales. Ils servent à déterminer la date des fêtes mobiles, de divers rites et de certaines conjonctions astronomiques. Les calendriers solaire et calendrier luni-solaires indiens s'inspirent d'approximations assez précises des heures d'entrée du Soleil dans les rasis successifs.

Les faiseurs d’almanach conservateurs continuent d'utiliser les formules et équations du Surya Siddhanta pour confectionner leurs ouvrages, appelés panchang. Ces panchangs sont des publications annuelles diffusées dans toutes les régions et tous les dialectes de l’Inde ; comme leurs homologues occidentaux, ils comportent toutes les dates des événements religieux, culturels et astronomiques de l'année en cours. Ils exercent une grande influence sur la vie religieuse et sociale des peuples de l'Inde, et on en trouve un exemplaire dans la plupart des foyers hindous.

Trigonométrie

Le Surya Siddhanta recourt à des rapports de longueur que l'on retrouve dans la trigonométrie à la Renaissance : ainsi le sinus d'un angle (appelé jya), son cosinus (kojya) et l’arcsinus (otkram jya) ; on y trouve aussi (versets 21–22 du 3^e chapitre), à propos de l'ombre portée par un gnomon sur le sol, la première utilisation de ce qu'on appelle aujourd'hui la tangente et la sécante d'un angle :

« Cherchez le jya (sinus) et le kojya (cosinus) de la distance zénithale de la méridienne solaire. Si le jya et le rayon sont multipliés, l'un par la taille du gnomon en chiffres, l'autre divisée par le kojya, on obtient l'ombre portée et l’hypoténuse à midi. »

En notation algébrique moderne, l'ombre portée par le gnomon à midi, s, est donc calculée selon :

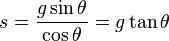
et l’hypoténuse h du gnomon à midi est calculée comme

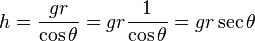
où est la taille du gnomon, son rayon, gnomon.

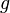
Éditions

Muhammad al-Fazari avait compilé dans son Grand Sindhind diverses œuvres en sanskrit, notamment le Surya Siddhanta et le Brahmasphutasiddhanta de Brahmagupta. Platon de Tibur le traduisit en latin en 1126.

• Ebenezer Burgess, « Translation of the Surya-Siddhanta, a text-book of Hindu Astronomy », dans Journal of the American Oriental Society, n^o 6, 1860, p. 141–498  .
• Surya Siddhanta: scans PDF de diverses éditions (en anglais et en sanskrit) , avec et sans les gloses en sansksrit...
• Ebenezer Burgess, Surya-Siddhanta: A Text Book of Hindu Astronomy, Kessinger Publishing, 1858 
• Surya-Siddhanta: A Text Book of Hindu Astronomy by Ebenezer Burgess Phanindralal Gangooly
• Surya Siddhanta texte en sanskrit transcrit en écriture devanagari.
• सूर्यसिद्धान्त (en Devanagari Unicode)