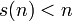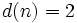Table des diviseurs - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
- Introduction - Légende des tables - Diviseurs des nombres de 101 à 200 - Diviseurs des nombres de 1 à 100 - Diviseurs des nombres de 301 à 400 - Diviseurs des nombres de 201 à 300 - Diviseurs des nombres de 501 à 600 - Diviseurs des nombres de 401 à 500 - Diviseurs des nombres de 701 à 800 - Diviseurs des nombres de 601 à 700 - Diviseurs des nombres de 901 à 1000 - Diviseurs des nombres de 801 à 900
Introduction
Les tables ci-dessous listent tous les diviseurs des nombres de 1 à 1000.
Un diviseur d'un nombre entier n est un entier m, exprimé n/m qui est de nouveau un entier (qui est aussi nécessairement un diviseur de n). Par exemple, 3 est un diviseur de 21, car 21/3 = 7 (et 7 est aussi un diviseur de 21).
Si m est un diviseur de n alors il est −m. Les tables ci-dessous listent seulement les diviseurs positifs.
Légende des tables
- d(n) est le nombre de diviseurs positifs de n, incluant 1 et n lui-même
- σ(n) est la somme de tous les diviseurs positifs de n, incluant 1 et n lui-même
- s(n) est la somme des diviseurs propres de n, qui n'inclut pas n lui-même
- Un nombre parfait égale la somme des diviseurs propres ; comme ceci :
-
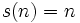
- Un nombre déficient est inférieur à la somme de ses diviseurs propres ; comme ceci :
- Un nombre abondant est supérieur à la somme de ses diviseurs propres ; comme ceci :
- Un nombre premier n'admet seulement 1 et lui-même comme diviseur s ; comme ceci :
Diviseurs des nombres de 101 à 200
| n | Diviseurs | d(n) | σ(n) | s(n) | Notes |
|---|---|---|---|---|---|
| 101 | 1, 101 | 2 | 102 | 1 | déficient, premier |
| 102 | 1, 2, 3, 6, 17, 34, 51, 102 | 8 | 216 | 114 | abondant |
| 103 | 1, 103 | 2 | 104 | 1 | déficient, premier |
| 104 | 1, 2, 4, 8, 13, 26, 52, 104 | 8 | 210 | 106 | abondant |
| 105 | 1, 3, 5, 7, 15, 21, 35, 105 | 8 | 192 | 87 | déficient |
| 106 | 1, 2, 53, 106 | 4 | 162 | 56 | déficient |
| 107 | 1, 107 | 2 | 108 | 1 | déficient, premier |
| 108 | 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108 | 12 | 280 | 172 | abondant |
| 109 | 1, 109 | 2 | 110 | 1 | déficient, premier |
| 110 | 1, 2, 5, 10, 11, 22, 55, 110 | 8 | 216 | 106 | déficient |
| 111 | 1, 3, 37, 111 | 4 | 152 | 41 | déficient |
| 112 | 1, 2, 4, 7, 8, 14, 16, 28, 56, 112 | 10 | 248 | 136 | abondant |
| 113 | 1, 113 | 2 | 114 | 1 | déficient, premier |
| 114 | 1, 2, 3, 6, 19, 38, 57, 114 | 8 | 240 | 126 | abondant |
| 115 | 1, 5, 23, 115 | 4 | 144 | 29 | déficient |
| 116 | 1, 2, 4, 29, 58, 116 | 6 | 210 | 94 | déficient |
| 117 | 1, 3, 9, 13, 39, 117 | 6 | 182 | 65 | déficient |
| 118 | 1, 2, 59, 118 | 4 | 180 | 62 | déficient |
| 119 | 1, 7, 17, 119 | 4 | 144 | 25 | déficient |
| 120 | 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120 | 16 | 360 | 240 | abondant |
| n | Diviseurs | d(n) | σ(n) | s(n) | Notes |
| 121 | 1, 11, 121 | 3 | 133 | 12 | déficient |
| 122 | 1, 2, 61, 122 | 4 | 186 | 64 | déficient |
| 123 | 1, 3, 41, 123 | 4 | 168 | 45 | déficient |
| 124 | 1, 2, 4, 31, 62, 124 | 6 | 224 | 100 | déficient |
| 125 | 1, 5, 25, 125 | 4 | 156 | 31 | déficient |
| 126 | 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126 | 12 | 312 | 186 | abondant |
| 127 | 1, 127 | 2 | 128 | 1 | déficient, premier |
| 128 | 1, 2, 4, 8, 16, 32, 64, 128 | 8 | 255 | 127 | déficient |
| 129 | 1, 3, 43, 129 | 4 | 176 | 47 | déficient |
| 130 | 1, 2, 5, 10, 13, 26, 65, 130 | 8 | 252 | 122 | déficient |
| 131 | 1, 131 | 2 | 132 | 1 | déficient, premier |
| 132 | 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132 | 12 | 336 | 204 | abondant |
| 133 | 1, 7, 19, 133 | 4 | 160 | 27 | déficient |
| 134 | 1, 2, 67, 134 | 4 | 204 | 70 | déficient |
| 135 | 1, 3, 5, 9, 15, 27, 45, 135 | 8 | 240 | 105 | déficient |
| 136 | 1, 2, 4, 8, 17, 34, 68, 136 | 8 | 270 | 134 | déficient |
| 137 | 1, 137 | 2 | 138 | 1 | déficient, premier |
| 138 | 1, 2, 3, 6, 23, 46, 69, 138 | 8 | 288 | 150 | abondant |
| 139 | 1, 139 | 2 | 140 | 1 | déficient, premier |
| 140 | 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140 | 12 | 336 | 196 | abondant |
| n | Diviseurs | d(n) | σ(n) | s(n) | Notes |
| 141 | 1, 3, 47, 141 | 4 | 192 | 51 | déficient |
| 142 | 1, 2, 71, 142 | 4 | 216 | 74 | déficient |
| 143 | 1, 11, 13, 143 | 4 | 168 | 25 | déficient |
| 144 | 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144 | 15 | 403 | 259 | abondant |
| 145 | 1, 5, 29, 145 | 4 | 180 | 35 | déficient |
| 146 | 1, 2, 73, 146 | 4 | 222 | 76 | déficient |
| 147 | 1, 3, 7, 21, 49, 147 | 6 | 228 | 81 | déficient |
| 148 | 1, 2, 4, 37, 74, 148 | 6 | 266 | 118 | déficient |
| 149 | 1, 149 | 2 | 150 | 1 | déficient, premier |
| 150 | 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150 | 12 | 372 | 222 | abondant |
| 151 | 1, 151 | 2 | 152 | 1 | déficient, premier |
| 152 | 1, 2, 4, 8, 19, 38, 76, 152 | 8 | 300 | 148 | déficient |
| 153 | 1, 3, 9, 17, 51, 153 | 6 | 234 | 81 | déficient |
| 154 | 1, 2, 7, 11, 14, 22, 77, 154 | 8 | 288 | 134 | déficient |
| 155 | 1, 5, 31, 155 | 4 | 192 | 37 | déficient |
| 156 | 1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78, 156 | 12 | 392 | 236 | abondant |
| 157 | 1, 157 | 2 | 158 | 1 | déficient, premier |
| 158 | 1, 2, 79, 158 | 4 | 240 | 82 | déficient |
| 159 | 1, 3, 53, 159 | 4 | 216 | 57 | déficient |
| 160 | 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, 160 | 12 | 378 | 218 | abondant |
| n | Diviseurs | d(n) | σ(n) | s(n) | Notes |
| 161 | 1, 7, 23, 161 | 4 | 192 | 31 | déficient |
| 162 | 1, 2, 3, 6, 9, 18, 27, 54, 81, 162 | 10 | 363 | 201 | abondant |
| 163 | 1, 163 | 2 | 164 | 1 | déficient, premier |
| 164 | 1, 2, 4, 41, 82, 164 | 6 | 294 | 130 | déficient |
| 165 | 1, 3, 5, 11, 15, 33, 55, 165 | 8 | 288 | 123 | déficient |
| 166 | 1, 2, 83, 166 | 4 | 252 | 86 | déficient |
| 167 | 1, 167 | 2 | 168 | 1 | déficient, premier |
| 168 | 1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 28, 42, 56, 84, 168 | 16 | 480 | 312 | abondant |
| 169 | 1, 13, 169 | 3 | 183 | 14 | déficient |
| 170 | 1, 2, 5, 10, 17, 34, 85, 170 | 8 | 324 | 154 | déficient |
| 171 | 1, 3, 9, 19, 57, 171 | 6 | 260 | 89 | déficient |
| 172 | 1, 2, 4, 43, 86, 172 | 6 | 308 | 136 | déficient |
| 173 | 1, 173 | 2 | 174 | 1 | déficient, premier |
| 174 | 1, 2, 3, 6, 29, 58, 87, 174 | 8 | 360 | 186 | abondant |
| 175 | 1, 5, 7, 25, 35, 175 | 6 | 248 | 73 | déficient |
| 176 | 1, 2, 4, 8, 11, 16, 22, 44, 88, 176 | 10 | 372 | 196 | abondant |
| 177 | 1, 3, 59, 177 | 4 | 240 | 63 | déficient |
| 178 | 1, 2, 89, 178 | 4 | 270 | 92 | déficient |
| 179 | 1, 179 | 2 | 180 | 1 | déficient, premier |
| 180 | 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180 | 18 | 546 | 366 | abondant |
| n | Diviseurs | d(n) | σ(n) | s(n) | Notes |
| 181 | 1, 181 | 2 | 182 | 1 | déficient, premier |
| 182 | 1, 2, 7, 13, 14, 26, 91, 182 | 8 | 336 | 154 | déficient |
| 183 | 1, 3, 61, 183 | 4 | 248 | 65 | déficient |
| 184 | 1, 2, 4, 8, 23, 46, 92, 184 | 8 | 360 | 176 | déficient |
| 185 | 1, 5, 37, 185 | 4 | 228 | 43 | déficient |
| 186 | 1, 2, 3, 6, 31, 62, 93, 186 | 8 | 384 | 198 | abondant |
| 187 | 1, 11, 17, 187 | 4 | 216 | 29 | déficient |
| 188 | 1, 2, 4, 47, 94, 188 | 6 | 336 | 148 | déficient |
| 189 | 1, 3, 7, 9, 21, 27, 63, 189 | 8 | 320 | 131 | déficient |
| 190 | 1, 2, 5, 10, 19, 38, 95, 190 | 8 | 360 | 170 | déficient |
| 191 | 1, 191 | 2 | 192 | 1 | déficient, premier |
| 192 | 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192 | 14 | 508 | 316 | abondant |
| 193 | 1, 193 | 2 | 194 | 1 | déficient, premier |
| 194 | 1, 2, 97, 194 | 4 | 294 | 100 | déficient |
| 195 | 1, 3, 5, 13, 15, 39, 65, 195 | 8 | 336 | 141 | déficient |
| 196 | 1, 2, 4, 7, 14, 28, 49, 98, 196 | 9 | 399 | 203 | abondant |
| 197 | 1, 197 | 2 | 198 | 1 | déficient, premier |
| 198 | 1, 2, 3, 6, 9, 11, 18, 22, 33, 66, 99, 198 | 12 | 468 | 270 | abondant |
| 199 | 1, 199 | 2 | 200 | 1 | déficient, premier |
| 200 | 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200 | 12 | 465 | 265 | abondant |
- Introduction - Légende des tables - Diviseurs des nombres de 101 à 200 - Diviseurs des nombres de 1 à 100 - Diviseurs des nombres de 301 à 400 - Diviseurs des nombres de 201 à 300 - Diviseurs des nombres de 501 à 600 - Diviseurs des nombres de 401 à 500 - Diviseurs des nombres de 701 à 800 - Diviseurs des nombres de 601 à 700 - Diviseurs des nombres de 901 à 1000 - Diviseurs des nombres de 801 à 900