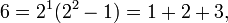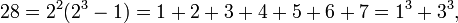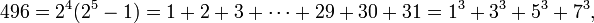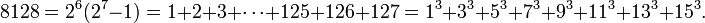Nombre parfait - Définition

Introduction

Un nombre parfait est un nombre naturel n non nul qui est égal à la somme de ses diviseurs stricts, autrement dit, tel que où σ(n) est la somme des diviseurs entiers positifs de n, n non compris.

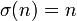
Le premier nombre parfait est 6, car 1, 2, et 3 sont les diviseurs stricts de 6 et 1 + 2 + 3 = 6.

Nombres parfaits pairs

Dans le Livre IX de ses Éléments, le mathématicien Euclide, au III^e siècle av. J.-C., a prouvé que si est premier, alors est parfait.

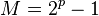
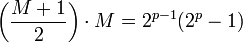
Ainsi :

• 6 = 2¹(2² − 1)
• 28 = 2²(2³ − 1)
• 496 = 2⁴(2⁵ − 1)
• 8128 = 2⁶(2⁷ − 1)
• ...

Par ailleurs, Leonhard Euler, au XVIII^e siècle, a prouvé que tout nombre parfait pair est de la forme proposée par Euclide. La recherche de nombres parfaits pairs est donc liée à celle des nombres premiers de Mersenne (nombres premiers de la forme 2^p-1).

Il est établi que tout nombre parfait pair se termine par un 6 ou un 8, mais pas forcément en alternance.

En 2000, Douglas Iannucci a démontré que tous les nombres pairs parfaits sont des nombres de Kaprekar en base deux.

Les nombres parfaits pairs étant de la forme 2ⁿ⁻¹(2ⁿ − 1), ce sont des nombres triangulaires, et, en tant que tels, la somme des entiers naturels jusqu'à un certain rang, en l'occurrence 2ⁿ − 1. De plus, tous les nombres parfaits pairs, excepté le premier, sont la somme des 2^(n−1)/2 premiers cubes impairs :

Le reste de la division d'un nombre parfait pair (à l'exception de 6) par 9 vaut 1. Ceci veut dire que le résidu d'un tel nombre vaut 1. Par exemple, le résidu de 8128 vaut 1, puisque 8 + 1 + 2 + 8 = 19, 1 + 9 = 10, et 1 + 0 = 1.

Exemples

Les 4 premiers nombres parfaits sont connus depuis l'antiquité. Depuis, le total est passé à 46 nombres parfaits seulement (au 7 octobre 2008).

Les douze premiers nombres parfaits sont :

• 6 = 1 + 2 + 3
• 28 = 1 + 2 + 4 + 7 + 14
• 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
• 8 128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1 016 + 2 032 + 4 064
• 33 550 336 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 + 1 024 + 2 048 + 4 096 + 8 191 + 16 382 + 32 764 + 65 528 + 131 056 + 262 112 + 524 224 + 1 048 448 + 2 096 896 + 4 193 792 + 8 387 584 + 16 775 168
• 8 589 869 056
• 137 438 691 328
• 2 305 843 008 139 952 128
• 2 658 455 991 569 831 744 654 692 615 953 842 176
• 191 561 942 608 236 107 294 793 378 084 303 638 130 997 321 548 169 216
• 13 164 036 458 569 648 337 239 753 460 458 722 910 223 472 318 386 943 117 783 728 128
• 14 474 011 154 664 524 427 946 373 126 085 988 481 573 677 491 474 835 889 066 354 349 131 199 152 128

Nombres parfaits impairs

En 2009, les mathématiciens ignorent si des nombres parfaits impairs existent. Différents travaux ont été entrepris mais aucun ne permet d'affirmer ou d'infirmer leur existence. Carl Pomerance a présenté une méthode heuristique qui suggère qu'aucun nombre parfait impair n'existe.

Un nombre parfait impair N doit remplir les conditions suivantes :

• N > 10³⁰⁰. Une recherche est en cours pour prouver que N > 10⁵⁰⁰.
• N est de la forme où :
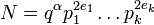
  • q, p₁, …, p_k sont des nombres premiers distincts (Euler) ;
  • q ≡ α ≡ 1 (modulo 4) (Euler) ;
  • Le plus petit facteur premier de N est inférieur à (2k + 8) / 3 (Grün 1952) ;
  • La relation e₁≡e₂≡...≡e_k ≡ 1 (modulo 3) n'est pas satisfaite (McDaniel 1970) ;
  • q^α > 10²⁰ ou > 10²⁰ pour j quelconque (Cohen 1987) ;
  • (Nielsen 2003).
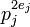
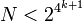
• Si e_i ≤ 2 pour tout i :
  • Le plus petit diviseur premier de N est au moins 739 (Cohen 1987) ;
  • α ≡ 1 (modulo 12) ou α ≡ 9 (modulo 12) (McDaniel 1970).
• Le plus grand diviseur premier de N est supérieur à 10⁸ (Takeshi Goto et Yasuo Ohno, 2006).
• Le second plus grand diviseur premier de N est supérieur à 10⁴ et le troisième est plus grand que 100 (Iannucci 1999, 2000).
• N comporte au moins 75 diviseurs premiers et au moins 9 diviseurs premiers distincts. Si 3 n'est pas un diviseur de N, alors N comporte au moins 12 diviseurs premiers distincts (Nielsen 2006 ; Kevin Hare 2005).