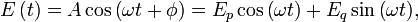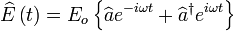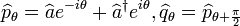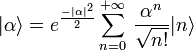Téléportation quantique - Définition
La liste des auteurs de cet article est disponible ici.
Téléportation quantique en variables continues
Aujourd’hui, ce protocole est implémenté en optique quantique dans le régime des variables dites continues par opposition au régime des variables discrètes abordé précédemment qui se caractérise entre autres par le comptage des photons. En effet, dans le régime des variables continues, on ne peut plus distinguer les photons individuellement : ils arrivent par « bouffées » contenant un très grand nombre de photons
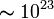
La première réalisation expérimentale d’une telle téléportation a été réalisée par l’équipe de H. J. Kimble au Caltech aux États-Unis par Akira Furusawa en 1998.
Avant d’aborder le principe de cette expérience qui, aujourd’hui est devenue routinière en optique quantique, il est utile de préciser quelques notions liées aux variables continues.
Expression d’un champ électrique monomode
Un champ électrique monomode s’écrit de manière classique comme :
qui est la décomposition usuelle du champ électrique dans le plan de Fresnel.
La procédure de quantification canonique conduit à associer au champ électrique l’opérateur suivant :
où les opérateurs
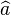
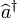
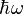
![\left[\widehat{a},\widehat{a}^{\dagger}\right] = 1](https://static.techno-science.net/illustration/Definitions/autres/2/285c5ab5602b42bdfeb67369b974b623_fc912808115b5faec6aefac7ee82d8dd.png)
La constante
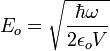
Opérateurs de quadrature
Ces opérateurs sont définis par analogie aux opérateurs de position et d’impulsion d’un oscillateur harmonique régi par les opérateurs de création et d’annihilation introduit précédemment. Ils seront définis de manière générale, en tenant compte d’une éventuelle rotation d’angle θ dans le plan de Fresnel, comme :
Pour le cas particuliers θ = φ, ces opérateurs correspondent respectivement aux quadratures d’amplitude et de phase du champ. Ainsi, leurs variances caractérisent respectivement les fluctuations d’amplitude et de phase. De plus, il est facile de vérifier que ces opérateurs ne commutent pas puisque
-
![\left[\widehat{p}_{\theta},\widehat{q}_{\theta} \right] = 2i](https://static.techno-science.net/illustration/Definitions/autres/0/02ba38324001359d7c32ac1bbe999b75_201fe49a1cf58c30066fde44cb3520d4.png)
On en déduit alors l'inégalité d’Heisenberg suivante :
-
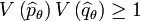
qui est très souvent employée sous la forme :
-
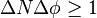
Autrement dit, lorsque l’on mesure avec précision le nombre de photons d’un faisceau, on brouille complètement la phase de ce dernier, et réciproquement.
Limite quantique standard et états cohérents du champ
L’opérateur d’annihilation
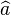
où α désigne un nombre complexe lié à l’amplitude A et à la phase φ du champ par α = Aeiφ.
Or, l’action des opérateurs de création et d’annihilation sur les états de Fock (i.e. état nombre de photon où il y a exactement n photons dans le mode considéré)
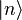
-
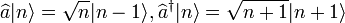
On vérifie alors facilement que :
Il est également utile de remarquer qu’un tel état cohérent du champ peut s’exprimer à partir de l’état vide de photons
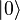
-
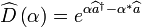
L’état cohérent, ou état quasi-classique de Glauber, s’écrira comme :
-
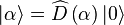
Ainsi, l’état vide de photons est un état cohérent dont la valeur moyenne de photons est nulle. Les fluctuations de cet état en amplitude et en phase définissent la limite quantique standard par rapport à laquelle on repère toute variance de bruit,
On voit bien qu’un état cohérent est affecté par des fluctuations qui sont identiques à celle du vide, puisqu’un état cohérent brillant n’est rien d’autres que l’état du vide déplacé dans le plan de Fresnel que l’on appelle aussi espace des phases.
Enfin, si l’on se rappelle l’inégalité d’Heisenberg qui contraint la mesure des quadratures d’amplitude et de phase, on constate qu’elle n’impose rien sur les variances individuelles. Il devient donc possible d’imaginer des faisceaux dont les fluctuations peuvent être « comprimés » selon l’une ou l’autre des quadratures. Il s’agit des états comprimés du rayonnement qui prennent une place importante dans les expériences d’optique quantique.