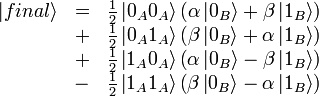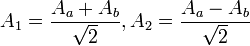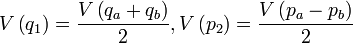Téléportation quantique - Définition
La liste des auteurs de cet article est disponible ici.
Protocole de téléportation quantique
Nous arrivons enfin au vif du sujet à savoir le principe de la téléportation quantique. Il est de tradition d’appeler les protagonistes d’un scénario de communication Alice et Bob. Alice dispose d’un qubit
-
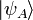
![\vert\phi^{+}_{AB}\rangle = \frac{1}{\sqrt{2}}\left[\vert 0_{A}0_{B}\rangle + \vert 1_{A}1_{B}\rangle \right] \neq \vert\phi_{A}\rangle\otimes\vert\phi_{B}\rangle](https://static.techno-science.net/illustration/Definitions/autres/f/fdb9688beac6baf7fb8d95e91c98eb82_a1c44827f933231cd7987507b31eff4b.png)
![\vert\phi^{+}_{AB}\rangle = \frac{1}{\sqrt{2}}\left[\vert 0_{A}0_{B}\rangle + \vert 1_{A}1_{B}\rangle \right] \neq \vert\phi_{A}\rangle\otimes\vert\phi_{B}\rangle](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/fdb9688beac6baf7fb8d95e91c98eb82_a1c44827f933231cd7987507b31eff4b.png)
En effet, pour un tel état, il est impossible de factoriser l’état de la paire de qubits sous la forme d’un produit tensoriel. Cette inséparabilité se traduit par de très fortes corrélations sur les résultats de mesure qu’il est impossible d’expliquer par des modèles classiques. On peut regarder à ce propos l’article sur l'expérience d'Aspect.
Alice qui souhaite communiquer à Bob l’état de son qubit sans être importunée par les indiscrétions d’Eve, applique à son qubit
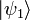
A) L’état initial du qubit d’Alice et de la paire intriquée s’écrit
-
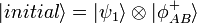
B) On fait interagir le qubit d’Alice avec le qubit EPR qu’elle détient via une porte cNOT dont le qubit de contrôle est le qubit d’Alice
![\vert inter. \rangle =\frac{\alpha}{\sqrt{2}}\vert 0_{A}\rangle\left[\vert 0_{A}0_{B}\rangle + \vert 1_{A}1_{B}\rangle\right]+\frac{\beta}{\sqrt{2}}\vert 1_{A}\rangle\left[\vert 1_{A}0_{B}\rangle + \vert 0_{A}1_{B}\rangle\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/ae05974951a152a2c1da383b6b74a491_fa50c41e89b610e6627ef1afa5deb340.png)
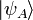
C) Ensuite, Alice fait subir à son qubit une opération d'Hadamard Hd qui donne le résultat final :
On constate alors que l’état du qubit d’Alice est téléporté sur le qubit de Bob dans 25 % des cas lorsque Alice mesure pour ces deux qubits les états binaires 0. Dans les autres cas, Alice doit transmettre à Bob le résultat de ces mesures, appelées mesures de Bell, afin que ce dernier puisse finaliser la téléportation. La théorie de la relativité restreinte d’Einstein n’est donc pas violée puisque la communication des résultats des mesures de Bell se fait par un canal classique. En effet, on montre sans difficulté que les états de Bob correspondant à chaque possibilité sont identiques à l’état du qubit d’Alice à une opération unitaire près. Par exemple, lorsque Alice projette ces deux qubits sur l’état
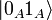
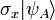
Compression et Intrication de faisceaux
Dans cette section, nous allons établir le lien très simple existant entre la compression de deux faisceaux et l’intrication de ces derniers. Pour celà, on considère deux faisceaux comprimés en amplitude selon des quadratures orthogonales en incidence sur une lame séparatrice 50/50 (SP). On notera A1 et A2 ces faisceaux incidents, et Aa et Ab les faisceaux émergents. La relation d'entrée sortie de la lame séparatrice donne :
Si les faisceaux incidents sont comprimés de manière adéquate, on trouve en termes des variances :
Dans le cas d'une compression en amplitude maximale (
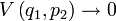
Enfin, il existe deux méthodes remarquables pour produire des états comprimés. Il s'agit de l'effet Kerr et de l'amplification paramétrique. Dans le premier cas, l'effet Kerr modifie la forme du disque des fluctuations du vide en une ellipse oblique globalement comprimée en amplitude. Pour l'amplification paramétrique, la configuration la plus efficace est de se placer sous le seuil d'oscillation (i.e. les pertes de la cavité ne sont plus compensées par la pompe) et en dégénerescence de fréquence. On obtient alors du vide comprimé en sortie.
