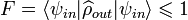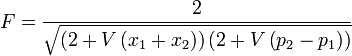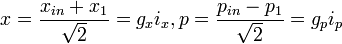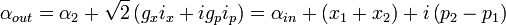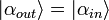Téléportation quantique - Définition

Critère de Téléportation Quantique

Il est nécessaire d'introduire un critère pour juger de la qualité d'une téléportation. Il s'agit de la fidélité F définie par :

où désigne la matrice densité caractérisant l'état téléporté. On montre que la fidelité de la téléportation est donnée par :

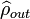
On constate que si l'on remplace les faisceaux EPR par des états cohérents, la fidélité atteint à peine 1/2 qui fixe la limite entre la téléportation classique utilisant des corrélations classiques et la téléportation quantique où le recours à l'intrication quantique est indispensable. D'autre part, une fidélité supérieure à 2/3 garantit l'unicité de la copie de Bob : aucune autre meilleure copie ne peut exister ! Il s'agit en fait d'une conséquence du théorème de non clonage quantique qui est à la base de la sécurité de ce genre de protocole de communication quantique.

Enfin, la première tentative de A. Zeilinger ne constitue pas vraiment une téléportation quantique comme l'ont remarqué H. J. Kimble et al dans un commentaire de l'article initial. En effet, le calcul de la fidélité de cette téléportation conduit à une valeur de 1/2, ce qui ne correspond pas à une téléportation quantique. Il existe également une réponse des autrichiens à ce commentaire.

Réalisation expérimentale d'une téléportation quantique bipartite

Nous allons maintenant aborder le principe de la téléportation quantique en variables continues comme l'illustre la figure.

Alice reçoit un faisceau d'amplitude complexe α_in = x_in + ip_in dont elle souhaite transférer à Bob l'état des quadratures x et p sans ajout de bruit. Pour celà, elle combine le faisceau à téléporter sur une lame séparatrice 50/50 (SP) avec un des faisceaux intriqués (1). Alice mesure les quadratures de phase x et d'amplitude p (à l'aide de détection homodyne) à la sortie de la séparatrice (SP) :

Ces résultats sont ensuite transmis à Bob par l'intermédiaire de canaux classiques, ici des courants électriques directement proportionnels aux résultats des mesures. Bob effectue alors des modulations de phase (MP) et d'amplitude (MA), à l'aide de modulateurs électro-optiques notamment, sur un faisceau annexe qu'il a en sa disposition au préalable. Il combine ce faisceau modulé à l'autre faisceau intriqué (2) à l'aide d'un miroir de très forte reflectivité (99 %). Bob dispose donc d'un faisceau de sortie dont l'amplitude complexe s'écrira :

Enfin, si les faisceaux (1) et (2) sont parfaitement intriqués :

,

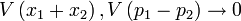
le faisceau de sortie se retrouve exactement dans l'état du faisceau d'entrée :

On parle alors de téléportation quantique des quadratures du champ.

Conclusions et perspectives

Actuellement, on s'attache à produire et à téléporter le plus fidèlement possible des états fortement non classiques comme des superpositions d'états cohérents incompatibles : "chats de Schrödinger" ou des états intriqués. Dans ce dernier cas, on parle de "entanglement swapping" pouvant atteindre des fidélités de l'ordre de 0.75 surpassant ainsi la valeur seuil de 2/3 liée au théorème de non clonage quantique. Enfin, le protocole de téléportation quantique s'inscrit dans une perspective plus ambitieuse consistant à la mise en œuvre de réseaux de communication quantique dans lesquelles on transfere l'état d'un système quantique fragile sur une mémoire quantique plus robuste vis à vis de la décohérence. D'intenses recherches se concentrent donc sur la réalisation de ces relais quantiques mais également sur les possibilités d'augmenter ou de distiller l'intrication de canaux EPR qui sont inévitablement soumis à des pertes en lignes. À partir de plusieurs canaux EPR affaiblis que l'on distille, on obtient un plus petit nombre de canaux plus fortement intriqués, rendant la téléportation quantique plus efficace et plus sûre^{[réf. souhaitée]}.