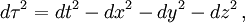Temps propre - Définition

Principe de maximisation de l'intervalle de temps propre

En se basant sur les propriétés de l'intervalle de temps propre John Wheeler et Edwin Taylor ont présenté une méthode, inspirée du principe de moindre action, qui permet de retrouver la plupart des résultats de la relativité générale sans faire appel au formalisme tensoriel et en utilisant uniquement l'algèbre élémentaire. Cette méthode permet par exemple de retrouver simplement les résultats d'Einstein sur la déviation des rayons lumineux au voisinage du Soleil et l'avance du périhélie de Mercure.

La méthode de Wheeler et Taylor est basée sur le principe suivant :

un mobile se déplaçant librement dans l'espace suit la trajectoire rendant maximale l'intervalle de temps propre.

Cette trajectoire est appelée géodésique de l'espace-temps considéré.

Pour se rappeler si le temps propre du mobile libre est maximal ou minimal on peut utiliser le moyen mnémotechnique du voyageur de Langevin. Dans cette expérience des jumeaux on sait que c'est le frère voyageur qui vieillit moins et le sédentaire qui vieillit plus. Donc l'intervalle de temps mesuré par le frère resté sur Terre est plus grand que l'intervalle mesuré par le frère monté dans la fusée. Or dans cette expérience, c'est bien la Terre qui représente le mobile libre car elle n'est soumise à aucune accélération, à aucun changement de direction. La fusée au contraire ne flotte pas librement dans l'espace (au moins pendant une partie de son trajet) puisqu'elle effectue notamment un demi-tour, ce qui ne peut pas être accompli sans allumer un moteur. Donc c'est bien le mobile libre qui mesure un temps propre maximal.

Dans la représentation sur un diagramme d'espace-temps du paradoxe des jumeaux, la ligne droite représente la ligne d'univers de la Terre, donc en fait la géodésique entre les deux événements départ et retour de la fusée, et c'est le long de cette ligne que le temps propre mesuré est le plus long. Réciproquement le fait que le voyageur en fusée ait mesuré un temps propre plus court que son frère prouve que lui n'a pas suivi une géodésique de l'espace-temps.

La géodésique entre deux événements est le trajet qui maximise le temps propre.

Fusion des unités de temps et d'espace

La relativité restreinte a opéré l'unification de l'espace et du temps en une seule structure à quatre dimensions : l'espace-temps. Il est donc normal de mesurer les temps et les longueurs avec la même unité. D'ailleurs, les unités de longueur et de temps ne sont plus des grandeurs indépendantes puisque le facteur de conversion entre les deux, c.-à-d. la vitesse de la lumière a été fixée à la valeur arbitraire de 299 792 458 m/s. En astronomie on a coutume de mesurer les distances en unités de lumière. Dire que telle étoile est située à dix années de lumière revient à dire que la lumière met dix années pour parvenir jusqu'à nous. Une seconde de lumière est la distance parcourue par la lumière en une seconde, soit 299 792 458 m. Une année faisant 365,25 jours, soit 3,2×10⁷ secondes, une année de lumière vaut 9,5×10¹⁵ mètres.

Les formules de conversion entre grandeurs exprimées en mètres et grandeurs exprimées en secondes sont :

r (en mètres) = r (en secondes)×c

r (en secondes) = r (en mètres)/c .

Les formules donnant la métrique de l'espace-temps prennent une forme plus simple dès que l'on mesure longueurs et temps soit en secondes soit en mètres puisque cela revient à prendre la vitesse c de la lumière égale à 1. En unités unifiées l'expression du carré du temps propre devient  :

et on ne « traîne » plus de facteurs c dans les formules. On comprend pourquoi les spécialistes de relativité préfèrent mener leurs calculs avec une vitesse de la lumière égale à l'unité.