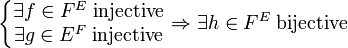Théorème de Cantor-Bernstein - Définition
La liste des auteurs de cet article est disponible ici.
Énoncé
S'il existe une injection f d'un ensemble E vers un ensemble F, et une injection g de l'ensemble F vers l'ensemble E, alors il existe une bijection h de E sur F.
Démonstration n° 3
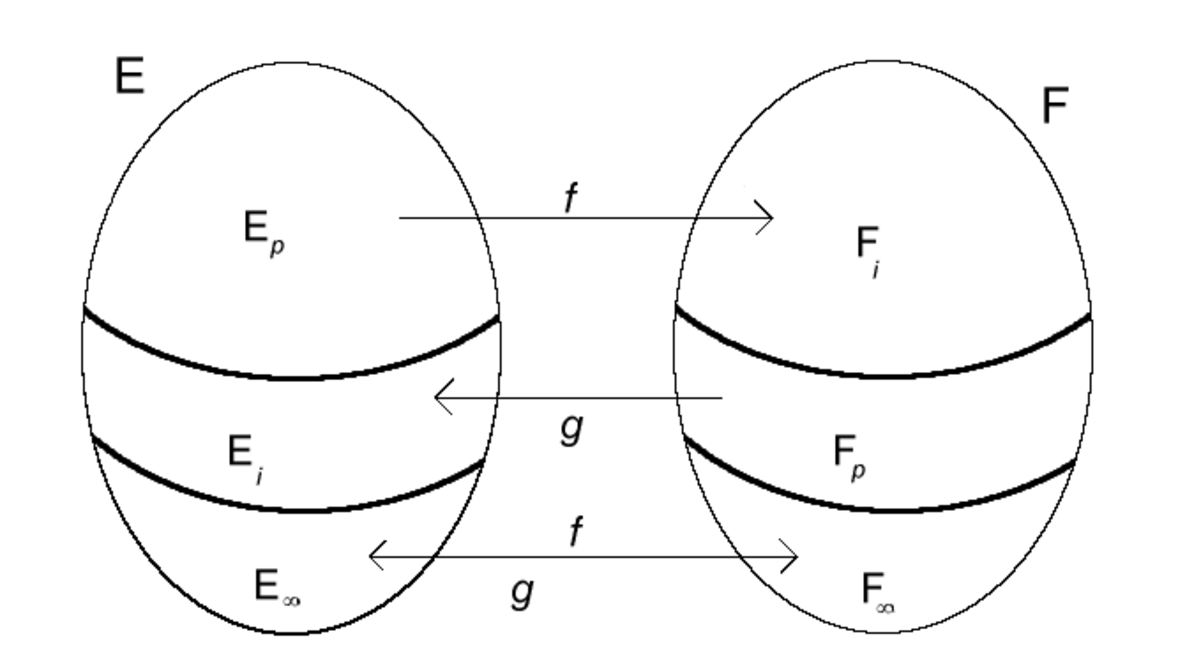
Appelons ancêtres d'un élément x de E l'antécédent de x par g (s'il existe) puis l'antécédent de cet antécédent par f, etc. Procédons de même pour les éléments de F.
Notons Ep (resp. Ei) l'ensemble des éléments de E ayant un nombre pair (resp. impair) d'ancêtres. Ep n'est autre que la partie C de la première démonstration. Notons
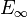
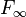
f est une bijection de Ep sur Fi et aussi de
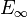
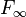
On peut ainsi construire une bijection de E sur F.
Démonstration n°2
Un lemme préliminaire
Cette démonstration repose sur le lemme suivant, cas particulier du théorème de Knaster-Tarski. Soit E un ensemble et
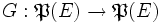
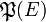
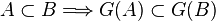
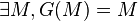
En effet, posons
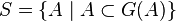
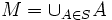
- pour tout
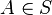
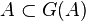
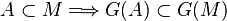
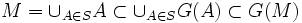
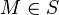
-
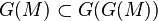
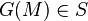
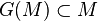
Démonstration finale
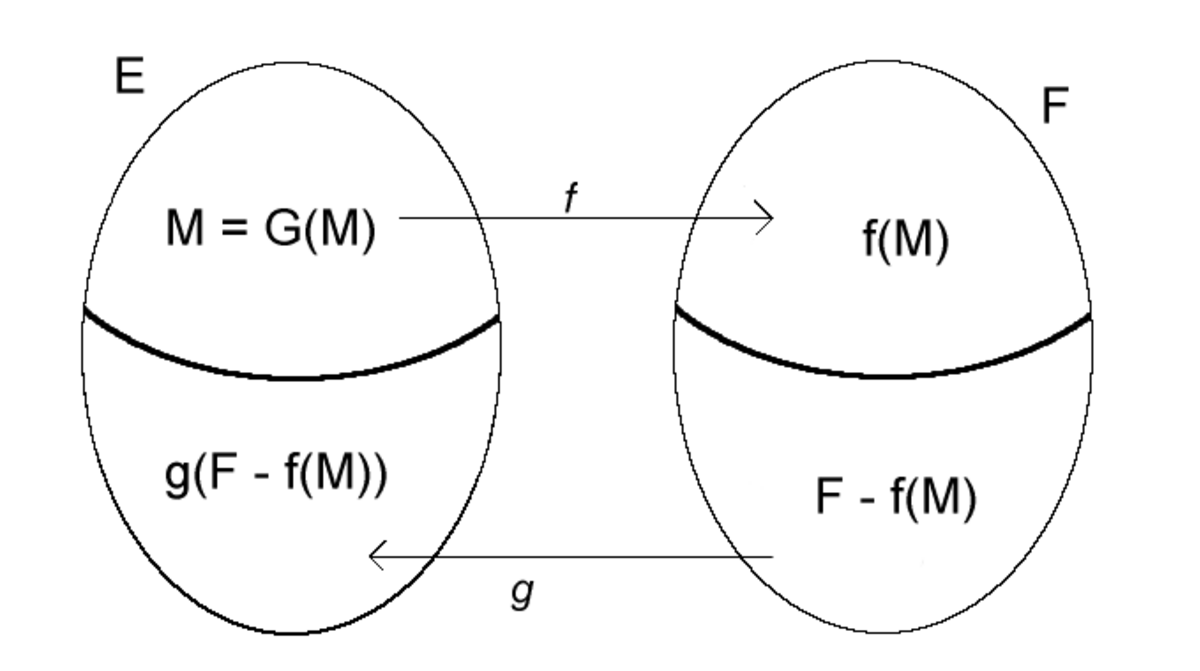
Soient maintenant f injective de E dans F et g injective de F dans E. Pour toute partie A de E, on pose
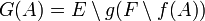
On introduit alors la partie M du lemme préliminaire. Cette partie est invariante par G ce qui signifie que g(F − f(M)) est exactement le complémentaire de M dans E.
On pose :
- si
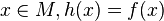
- si
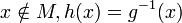
h est bijective de E dans F.
M joue un rôle comparable à la partie C dans la première démonstration ou à
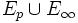
Généralisation
Soient X un ensemble non vide et
- si
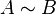
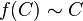
- si
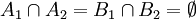
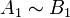
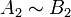
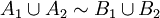
Soient deux ensembles A et B, un sous-ensemble A1 de A et un sous-ensemble B1 de B. On suppose que
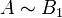
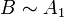
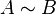
Ceci peut également être démontré sans l'axiome du choix. Dans le cas particulier où
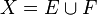
Références
- Casiro F, Le Théorème de Cantor-Bernstein, Tangente, mai-juin 2008, p42-44
- Stan WAGON, The Banach-Tarski Paradox, Editions Cambridge University Press, ISBN 0-521-45704-1
Applications
Si l'on considère la technique naïve qu'a un enfant pour compter le nombre d'éléments d'un ensemble, cela revient quasiment toujours à associer chacun des élements à un autre d'un ensemble connu dont le nombre d'éléments est connu.
Il peut s'agir soit d'associer chacun des éléments à compter avec l'un des doigts, soit d'associer chacun des éléments avec un nombre que l'on réciterait à haute voix (un, deux, trois, etc.), par exemple.
En clair, compter se fait naïvement en effectuant une bijection d'un ensemble dont la « dimension » est connue vers un autre dont la dimension est inconnue.
Ce théorème s'interprète alors comme disant : « Si je peux compter une partie d'un ensemble avec la totalité des éléments d'un autre ensemble, et réciproquement, alors ils ont le même nombre d'éléments ». Ce qui est évident pour des ensembles finis. Ce théorème généralise alors cette notion pour des ensembles infinis.
- Si je peux compter un certain nombre de billes de mon sac de billes avec mes dix doigts, et qu'avec la totalité de mes billes, je peux les associer avec certains de mes doigts, alors j'ai exactement dix billes.
À partir de là, ce théorème représente l'une des briques de base pour généraliser la notion de tailles d'ensembles à des ensembles infinis.