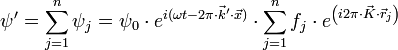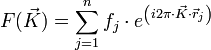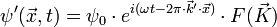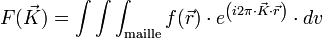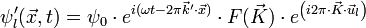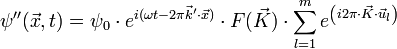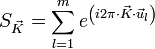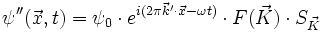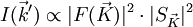Théorie de la diffraction sur un cristal - Définition

Influence de l'organisation de la matière

Facteur de structure

Facteur de structure : interférence des ondes diffusées par les atomes de la maille

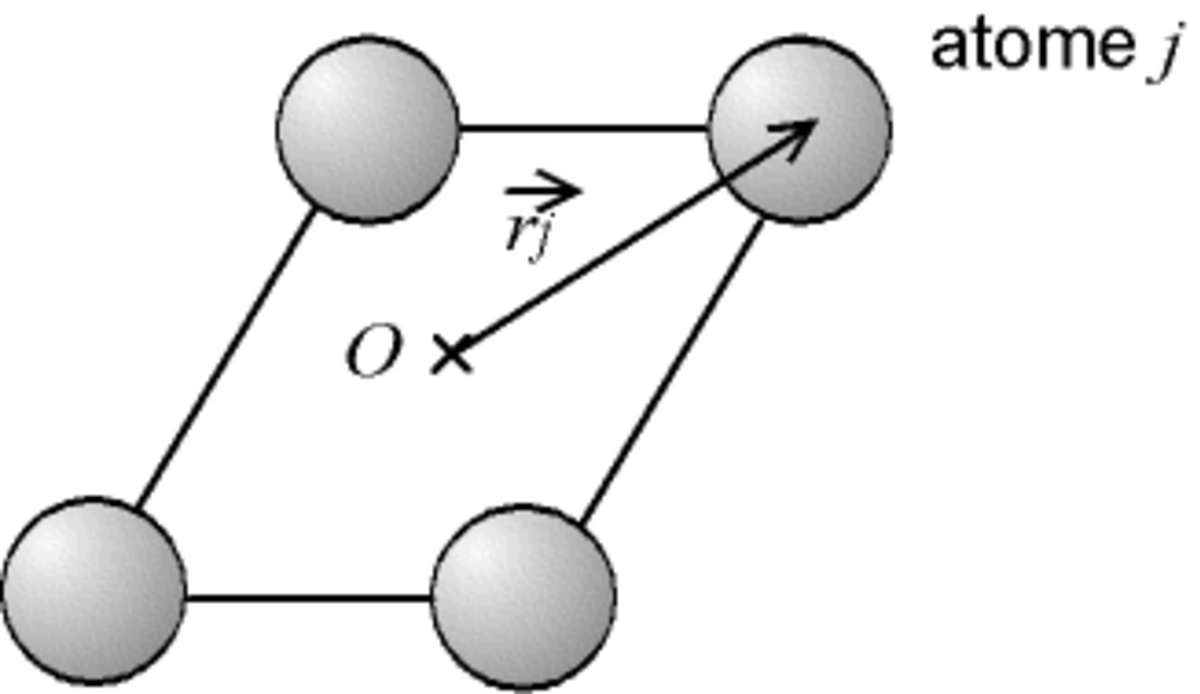
On peut maintenant se placer non plus à l'échelle d'un atome, mais à l'échelle d'une maille cristalline. L'onde ψ' diffractée par la maille est la somme des ondes diffusées par chacun de ses n atomes :

On définit le facteur de structure F comme étant :

on a donc

On a considéré ici que l'onde était diffusée par un atome ponctuel. En toute rigueur, dans le cas de la diffracion de rayons X, l'onde est diffusée par le nuage électronique, qui est une fonction continue de l'espace. Il faut donc définir en chaque point de la maille un facteur de diffusion local , le facteur de structure s'écrivant alors :

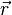
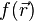
dv étant l'élément de volume considéré autour de la position .

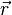
On voit ainsi que le facteur de structure est la transformée de Fourier de la distribution électronique(pour les rayons X) dans la maille élémentaire.

Facteur de forme

Facteur de forme : interférence des ondes diffractées par les différentes mailles du cristallite

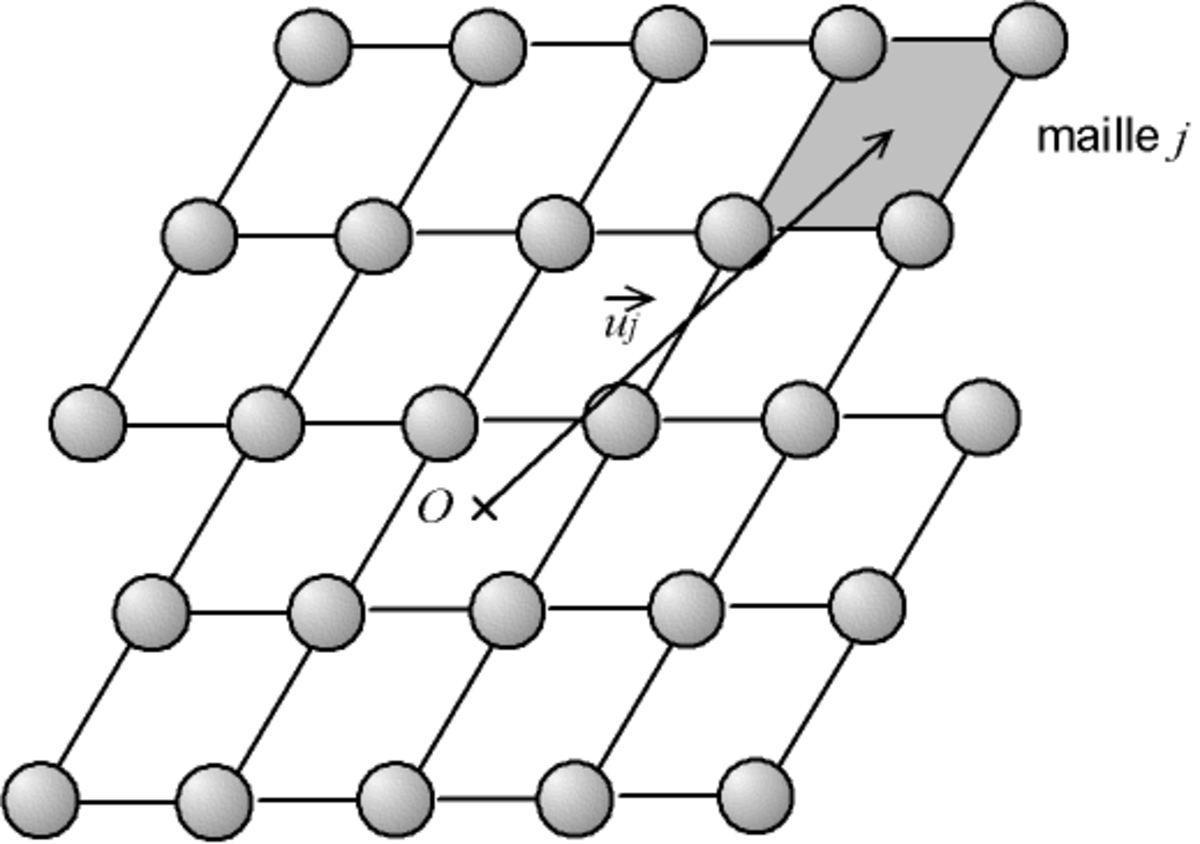
Le cristal est composé de m mailles. La fonction ψ'_l de l'onde diffractée par une maille l placée en s'écrit :

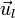
(ceci se montre de manière similaire à précédemment en considérant le déphasage entre la source et la maille, puis entre la maille et le point ).

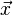
L'onde ψ'' diffractée par l'ensemble du cristal est la somme des ondes diffractées par chaque maille, soit :

On définit le facteur de forme par :

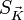
on a donc

dépend de la forme du cristal, d'où son nom. C'est ce facteur qui intervient dans l'élargissement des raies lorsque la taille des cristallites est faible (inférieure à 1 μm).

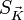
Intensité diffractée

L'intensité diffractée I dans un point de l'espace est proportionnelle au carré de la norme du vecteur de la fonction d'onde :

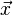
On a un effet d'atténuation en fonction de l'éloignement qui varie selon l'inverse du carré de la distance : il s'agit simplement de la « répartition » de l'énergie sur une sphère (dimunution de la densité angulaire). Si l'on corrige ce phénomène, alors l'intensité ne dépend que de la direction de l'espace, que l'on peut donner par le vecteur de l'onde diffractée  :

avec fixé arbitrairement,

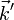
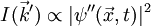
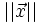
soit

D'autres facteurs interviennent, notamment la géométrie de l'appareil de mesure, l'optique. Par exemple, l'intensité peut varier selon l'inclinaison du détecteur par rapport à l'échantillon.

Théorie cinétique et théorie dynamique

Nous avons exposé ci-dessus la théorie dite « cinétique » de la diffraction. Dans la théorie cinétique, on considère que l'onde diffusée par les nœuds ne diffracte pas elle-même. Cette hypothèse est valable lorsque l'intensité diffractée est faible devant l'intensité incidente, ce qui est le cas avec les rayons X et les neutrons.

Cette hypothèse n'est en général plus valable avec les électrons, sauf dans le cas de la diffraction par une lame mince (dans un microscope électronique en transmission). On a alors recours à la théorie dite « dynamique ».