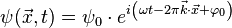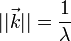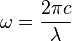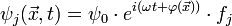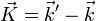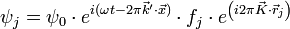Théorie de la diffraction sur un cristal - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La théorie de la diffraction sur un cristal modélise l'interaction rayonnement-matière dans le cas où la matière est organisée de manière ordonnée (voir aussi Cristallographie).
Ces phénomènes interviennent essentiellement dans les méthodes d'analyse et d'observation de la matière :
- diffraction des électrons en microscopie électronique en transmission ;
- diffractométrie de rayons X ;
- diffraction de neutrons.
On peut en avoir une approche simplifiée purement géométrique avec l'analogie avec un réseau de diffraction et la loi de Bragg.
Dans une large mesure, l'analyse est indépendante de la nature de la radiation incidente : rayonnement électromagnétique (rayons X) ou particule (électrons, neutrons). Toutefois, la nature du rayonnement intervient pour une analyse plus fine.
Diffusion par les atomes
Le phénomène à la base de la diffraction par un cristal est la diffusion du rayonnement par les atomes. On considère exclusivement une diffusion élastique (le rayonnement ne perd pas d'énergie), il s'agit donc de diffusion Rayleigh.
Cette diffusion est anisotrope ; toutefois, pour une première approche, on peut considérer par approximation que cette diffusion est isotrope, c'est-à-dire que l'intensité diffusée par chaque atome est indépendante de la direction de l'espace.
Pour simplifier, on considère un rayonnement monochromatique. Le rayonnement de longueur d'onde λ peut être décrit par sa fonction d'onde ψ en tout point
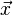
où φ0 est la phase à l'origine spatiale et temporelle,

et ω est la pulsation
c étant la vitesse de la lumière.
On choisit arbitrairement l'origine telle que φ0 = 0.
Une maille donnée du cristal est composée de n atomes. Chaque atome j placé en
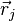
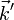
-
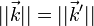
- la direction de
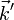
La fonction de l'onde diffusée par l'atome j est ψj et s'écrit :
où φ est le déphasage de l'onde en
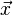
Le déphasage φ est la somme de deux contributions :
- au point
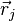
-
-
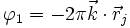
-
- le déphasage φ2 de l'onde diffractée entre sa source (l'atome en
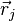
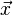
-
-
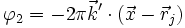
-
- le déphasage total vaut
-
-
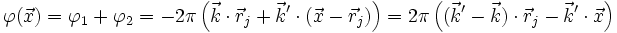
-
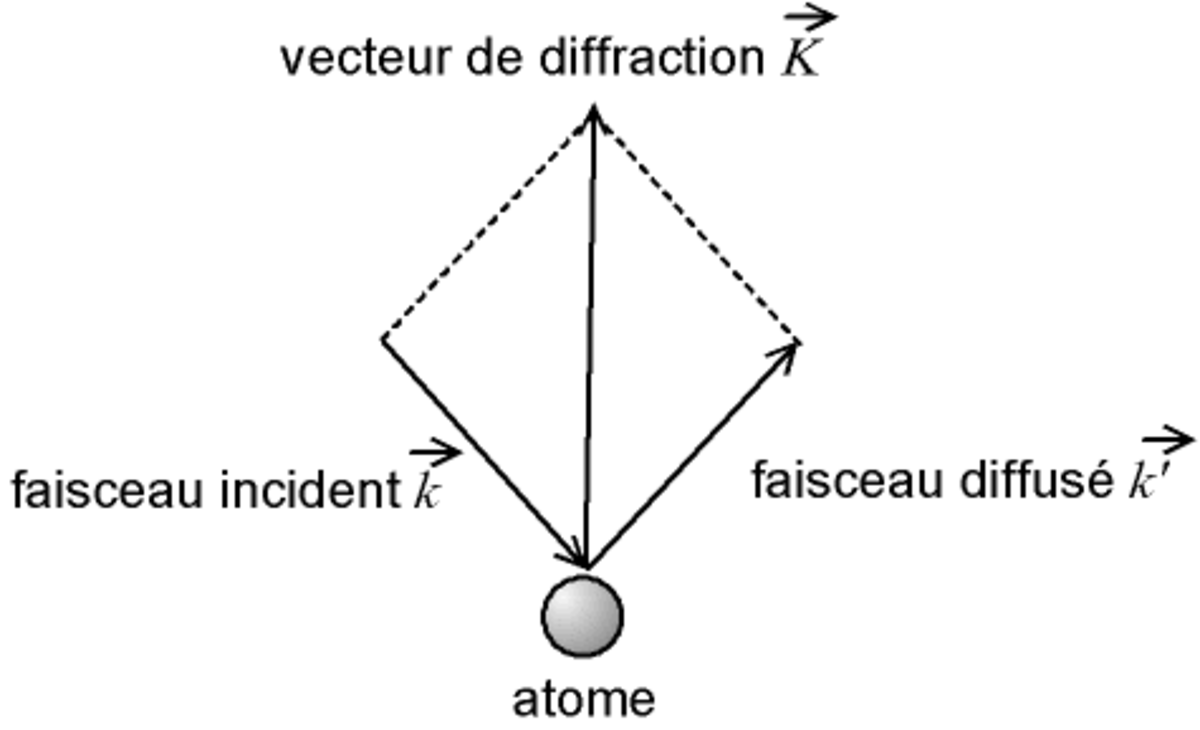
Si l'on définit le vecteur de diffraction

on a alors :
- Note
- On ne considère qu'une direction de diffusion à la fois, la « direction d'observation » (par exemple direction dans laquelle se trouve le détecteur ponctuel de rayonnement servant à la mesure ou emplacement donné du film photographique ou du détecteur à résolution spatiale), et donc qu'un seul vecteur de diffraction ; mais l'onde est bel et bien diffusée dans toutes les directions simultanément.