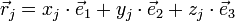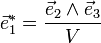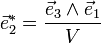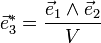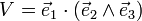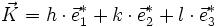Théorie de la diffraction sur un cristal - Définition

Conditions de diffraction

Condition de Laue

Dans un diagramme de diffraction, un pic (ou un point si c'est une figure 2D) correspond à un maximum d'intensité, c'est-à-dire à un maximum local de F. Intuitivement, F est maximal lorsque les rayons diffusés par les atomes de la cellule sont tous en phase. Si l'on considère deux atomes j et l, on doit avoir

(eq1)

Soit la base du réseau direct ; les positions des atomes s'écrivent

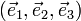
où x_j, y_j et z_j sont des nombres entiers.

Considérons la base de l'espace réciproque avec

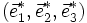
V étant le volume de la maille

Obtenir la condition générale de diffraction revient à appliquer la condition () à tous les atomes de la maille deux à deux. On peut montrer que cela impose aux produits scalaires d'être entiers (i = 1,2,3). Or les relations de définition de la base réciproque ci-dessus imposent

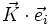
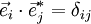
et par conséquent, si l'on écrit le vecteur de diffraction comme une combinaison linéaire à coefficients entiers des vecteurs de la base réciproque, alors ses composantes dans la base directe sont bien entières. On définit donc (h,k,l) entiers tels que :

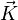
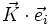
L'équation ci-dessus est la condition de diffraction de Laue (dont on peut montrer qu'elle est équivalente à la condition de Bragg.). On interprète les nombres (h k l) comme étant des indices de Miller : si le faisceau incident est de direction constante ( constant), cela revient à dire que les directions de diffraction donnant un maximum d'intensité sont telles que les sont orthogonaux aux plans (h k l), puisqu'on sait que les rangées [h k l]*, définies par leur colinéarité à , sont orthogonales aux plans (h k l).

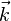
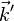
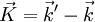
On peut ainsi indexer les vecteurs d'onde donnant des maxima d'intensité par les indices de Miller et écrire . On peut également indexer les facteurs de structure correspondants :

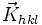
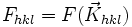
Les lieux des extrémités des forment un réseau dans l'espace réciproque, appelé réseau réciproque. On peut donc associer chaque point du réseau réciproque (c'est-à-dire chaque vecteur ) à un plan cristallographique, d'indices de Miller (h k l), plan perpendiculaire à .

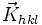
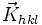
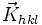
Remarque : On définit les indices de Miller h, k, l comme devant être premiers entre eux, les vecteurs (où (h', k', l')=i(h,k,l), i étant un entier relatif) se rapportent tous aux mêmes indices h, k, l, ou encore à une direction [h k l]*, à laquelle une infinité de rangées de points de l'espace réciproque sont parallèles. On peut donc maintenant associer à une famille de rangées parallèles d'indices [h k l]* une famille de plans parallèles d'indices (h k l). Ce choix d'indices de Miller premiers entre eux traduit le fait qu'en cristallographie on s'intéresse aux directions (plans et rangées) dans le cristal et non à un plan ou à une rangée particulière dans le cristal.

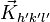
En pratique, lors d'une expérience de diffraction des rayons X, on obtient une figure de diffraction (cliché de Laue par exemple), sur laquelle on visualise les maxima d'intensité. On peut montrer que les symétries d'un réseau direct (associé au cristal) sont les mêmes que celles du réseau réciproque associé (associé aux directions de diffraction) : cela signifie que les symétries de la figure de diffraction doivent se retrouver parmi les symétries du cristal.

Une méthode graphique pour trouver les vecteurs de diffraction : la sphère d'Ewald

Selon la condition de Laue, il y a diffraction si

(eq2)

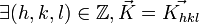
donc si est un vecteur du réseau réciproque d'un des cristallites éclairés.

Géométrie de Bragg-Brentano

Symétrie des vecteurs d'onde lorsque le vecteur de diffraction garde la même direction

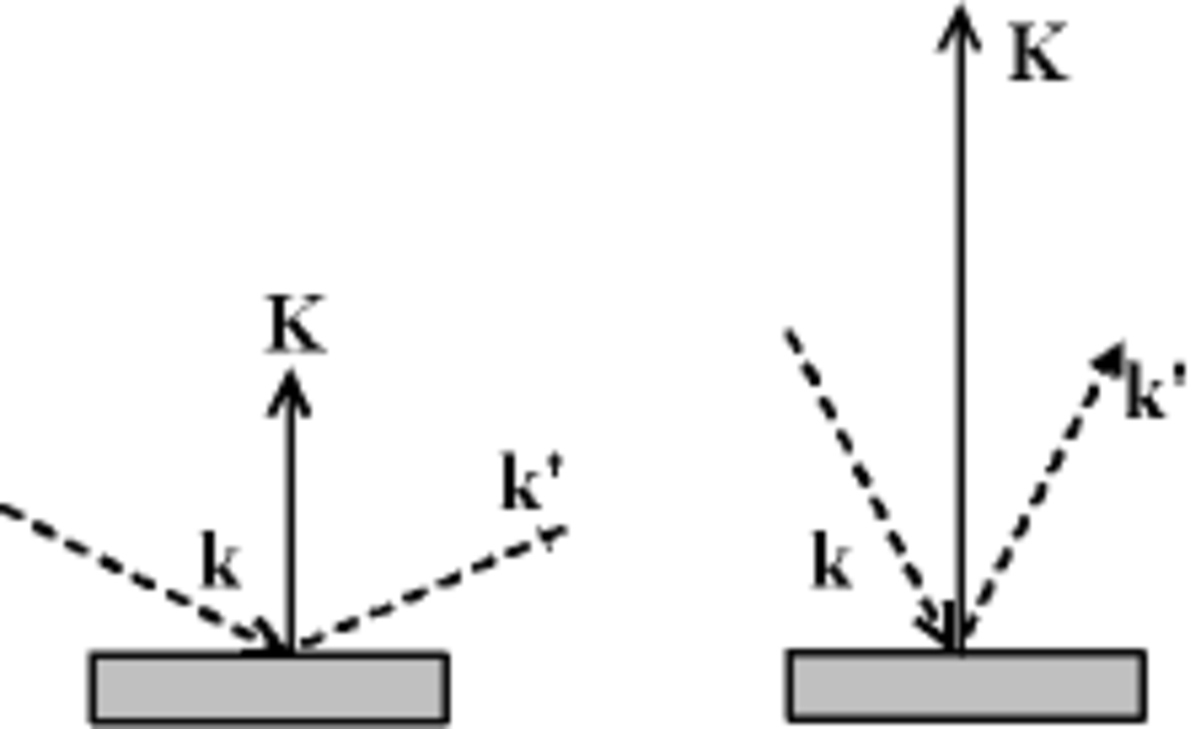
Etudions uniquement le cas où le vecteur de diffraction garde toujours la même orientation par rapport au cristallite (la bissectrice entre le faisceau incident et la direction d'observation est toujours sur la même droite) ; cela signifie que les vecteurs de l'onde incidente et de l'onde diffusée sont toujours symétriques par rapport à cette direction, dans l'espace réel comme dans l'espace réciproque. Cela correspond à la géométrie de Bragg-Brentano, on place le détecteur de manière symétrique à la normale à l'échantillon passant par le centre de celui-ci.

Plaçons-nous dans le cas d'un monocristal. On voit que selon la déviation du faisceau, c'est-à-dire l'angle que fait le faisceau incident avec la direction d'observation, on est en condition de diffraction ou pas.

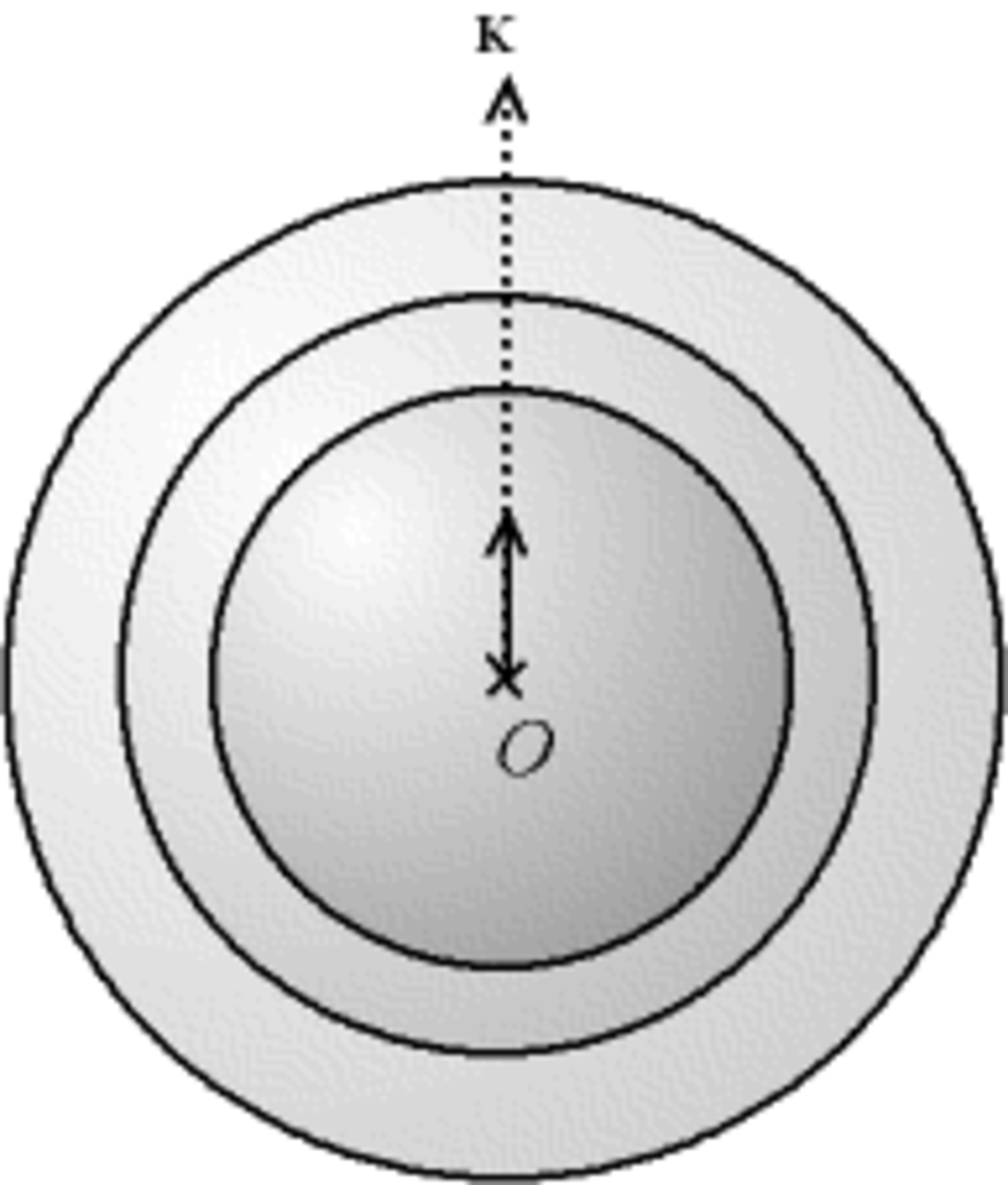
Supposons maintenant que l'on fasse tourner le cristallite dans tous les sens durant la mesure, ou, ce qui est équivalent, que l'échantillon soit constitué d'une multitude de cristallites orientés dans tous les sens (poudre). Alors, il faut superposer tous les réseaux réciproques pour connaître les déviations donnant un pic/point de diffraction. Cela donne des sphères concentriques ; il y a diffraction si le vecteur de diffraction rencontre une sphère.

Vecteur de diffraction et réseau réciproque d'un monocristal

Sphères formées par la superposition des réseaux réciproques des cristallites d'une poudre

Incidence fixe

Sphère d'Ewald : positions possibles de l'extrémité du vecteur de diffraction lorsque l'incidence est fixe, cas d'un monocristal

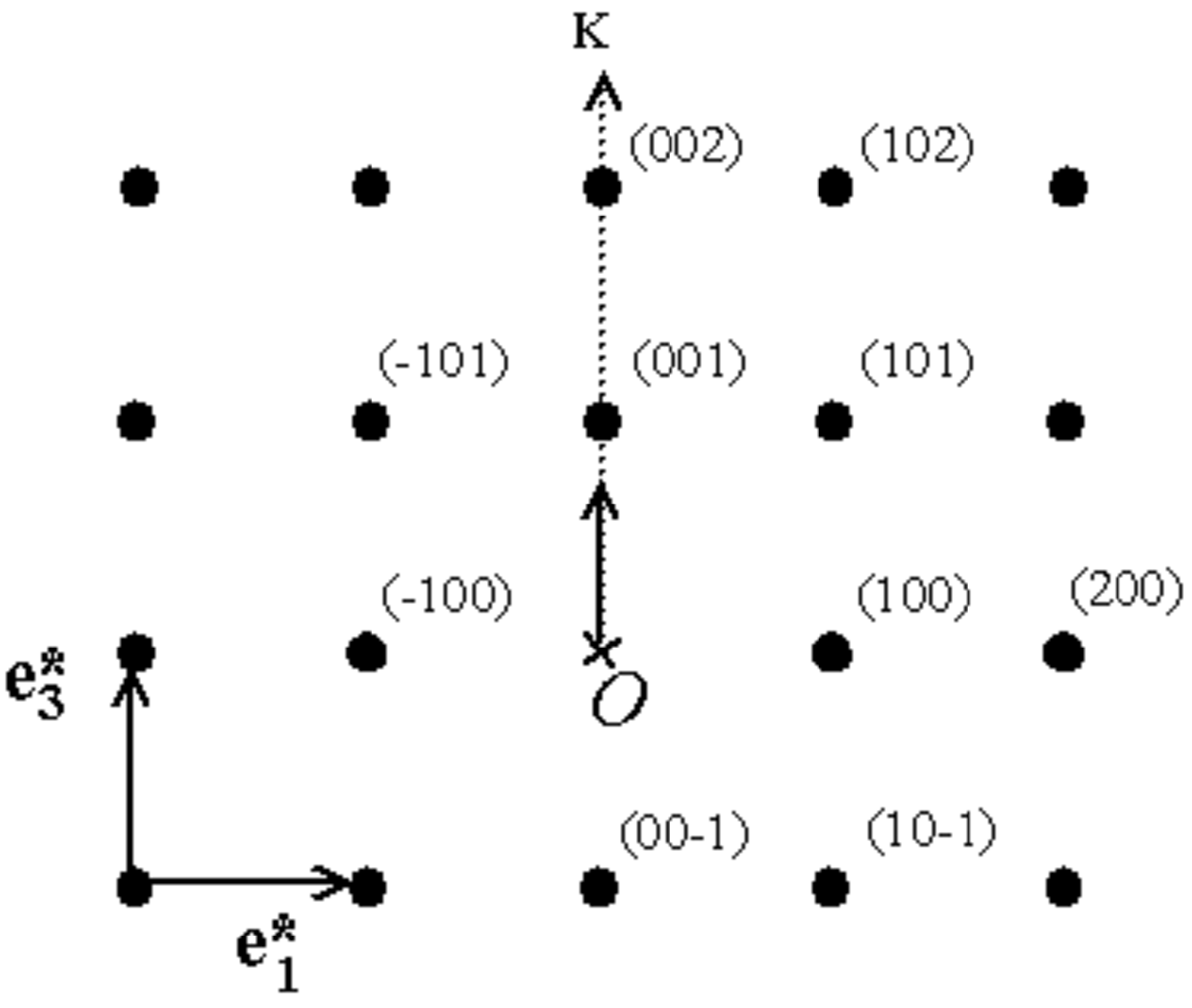
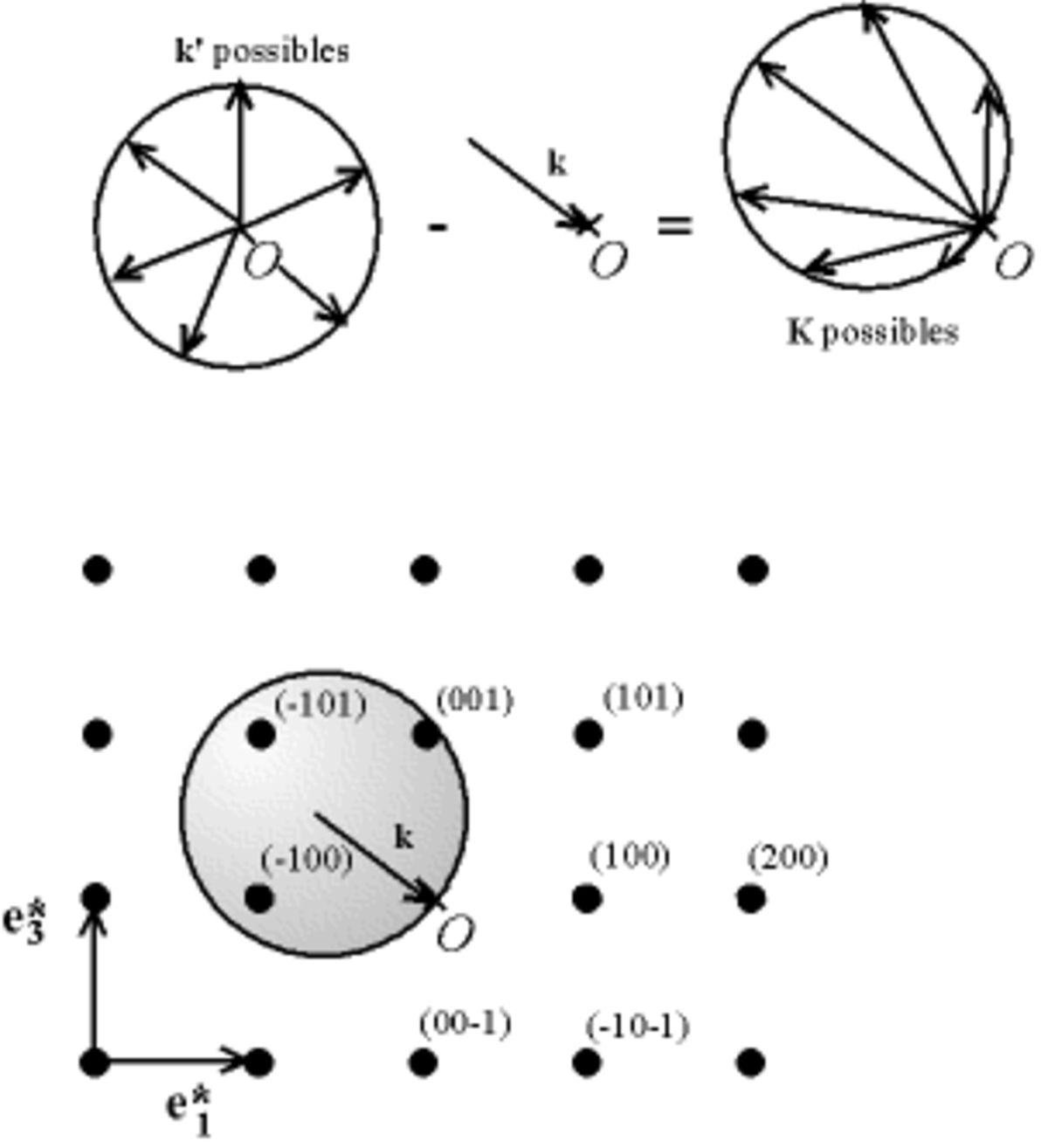
Considérons qu'à un instant donné, le vecteur de l'onde incidente est toujours le même (la position de l'échantillon par rapport à la source ne change pas et la source est ponctuelle). On n'impose pas ici de direction d'observation, le vecteur de l'onde diffusée peut donc prendre toutes les orientations possibles, mais il a toujours la même norme ; il décrit donc une sphère de rayon 1/λ. Les vecteurs de diffraction possibles forment donc une sphère de même rayon mais dont le centre est situé en par rapport à l'origine du réseau réciproque, par définition du vecteur de diffraction. Cette sphère s'appelle la « sphère d'Ewald » (ou « sphère de réflexion »), et elle contient l'origine O du réseau réciproque.

L'intersection de la sphère des nœuds des réseaux réciproques (dans le cas d'une poudre) des cristallites et de la sphère d'Ewald étant un cercle, les vecteurs des ondes diffusées en condition de diffraction forment un cône

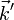
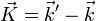
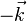
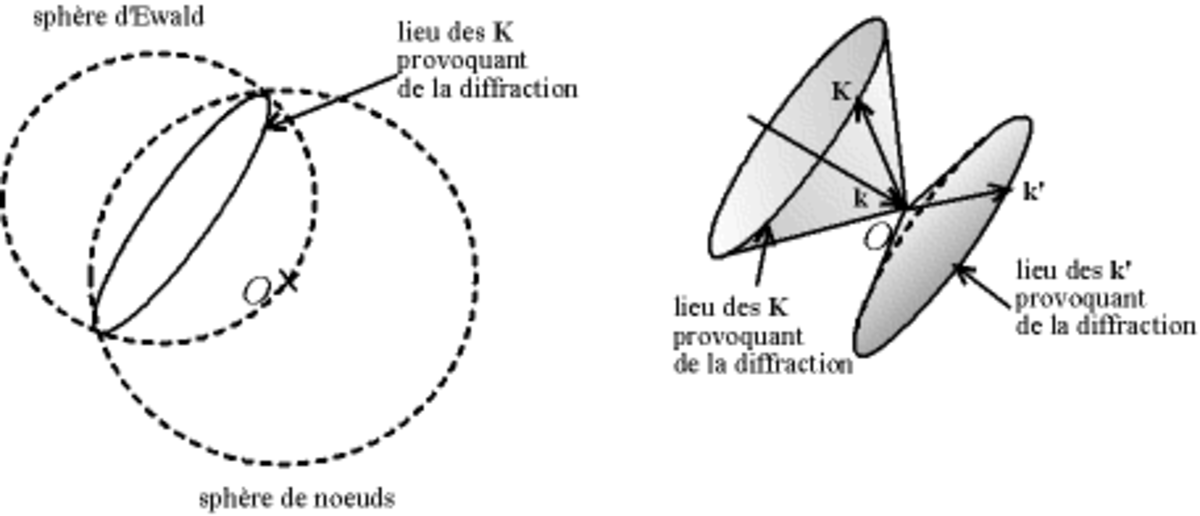
Les directions dans lesquelles on aura de la diffraction sont donc données par l'intersection de la sphère d'Ewald avec les sphères des . L'intersection de deux sphères non concentriques, lorsqu'elle existe, est un cercle. On en déduit que les extrémités des vecteurs de diffraction pour lesquels il y a diffraction forment un cercle, donc que les extrémités des vecteurs d'onde diffusée pour lesquels il y a diffraction décrivent un cercle, c'est-à-dire que : les rayons diffractés forment des cônes.

Sphère de résolution, obtenue par la rotation de la sphère d'Ewald autour de l'origine ; son rayon vaut 2/λ

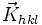
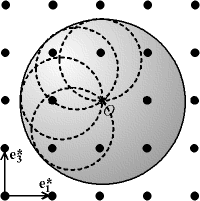
Considérons maintenant que l'on garde le réseau réciproque immobile (monocristal), mais que l'on fait tourner la sphère d'Ewald. On voit que la sphère d'Ewald va balayer une boule de centre O et dont le rayon est le diamètre de la sphère d'Ewald. Les points contenus dans cette « supersphère » correspondent aux différentes conditions de diffraction possibles ; les points à l'extérieur ne peuvent pas, dans les conditions de mesure données (c'est-à-dire pour la longueur d'onde λ donnée), donner de diffraction. Cette « supersphère » est appelée « sphère de résolution », elle a un rayon de 2/λ.

Si λ est trop grand, la sphère de résolution ne contient que le centre du réseau réciproque, la diffraction n'est donc pas possible. C'est la raison pour laquelle il faut recourir à des rayonnement de longueur d'onde suffisamment petite (rayons X ou particules ayant une vitesse suffisamment élevée) pour pouvoir caractériser un réseau cristallin.

Rotation de la sphère d'Ewald et géométrie de Bragg-Brentano (direction du vecteur de diffraction imposée)

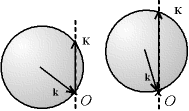
Si l'on se remet dans une géométrie de Bragg-Brentano (direction du vecteur de diffraction fixée), le vecteur de diffraction est obtenu en prenant l'intersection de la sphère avec l'axe de la direction imposée.

Facteur de forme et réseau réciproque

Pour les conditions de diffraction, nous n'avons considéré jusqu'ici que le facteur de structure. Les conditions de diffraction pour un monocristal se représentent comme un réseau ponctuel dans l'espace réciproque.

Ceci ne serait vrai que pour un monocristal de dimension « infinie ». Pour un cristallite de taille finie, on a une diffraction au sens diffraction de Fraunhofer ; sur un film photographique, la trace de diffraction n'est donc pas un ensemble de points infiniment petits, mais des taches d'Airy.

Dans l'espace réciproque, la condition de diffraction n'est pas un réseau de points, mais un réseau de taches tridimensionnelles.

La forme de ces taches dans l'espace réciproque est décrite par le facteur de forme. De manière classique en matière de diffraction, la tache du réseau réciproque est plus étendue dans la direction perpendiculaire à la dimension la plus étroite du cristallite.

Si le cristallite est sphérique mais de petite taille (inférieure au micromètre), la tache dans l'espace réciproque sera de symétrie sphérique, la densité décroissant avec le rayon (l'intensité diffractée étant proportionnelle à cette densité).

Si le cristallite est un disque (cylindre aplati dans son axe), la tache de diffraction sera une aiguille (cylindre de faible rayon mais étiré selon son axe).