Théorie de la fonctionnelle de la densité - Définition
La liste des auteurs de cet article est disponible ici.
Modèle de Thomas-Fermi
La Théorie de la Fonctionnelle de la Densité tire ses origines du modèle de Thomas-Fermi , développé par Llewellyn Thomas et Enrico Fermi en 1927. La méthode de Thomas-Fermi repose sur un modèle statistique afin d’approximer la distribution électronique autour d’un atome. La base mathématique utilisée était de postuler que les électrons sont distribués de manière uniforme dans l’espace des phases, avec deux électrons dans chaque h3 de volume. Pour chaque élément de coordonnées de l’espace volumique d3r il est possible de remplir une sphère d’espace de mouvement jusqu’au mouvement de Fermi pf.
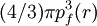
La mise en équation du nombre d’électrons en coordonnées spatiales dans cet espace des phases donne :
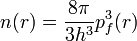
La résolution de cette équation pour pf et sa substitution dans la formule de l’énergie cinétique classique conduit directement à l’obtention d’une énergie cinétique, représentée comme une fonctionnelle de la densité électronique :
![T_{TF}[n]=\frac{3}{10}(3\pi^2)^{2/3}\int n^{5/3}(r) d^3r.](https://static.techno-science.net/illustration/Definitions/autres/f/fd5926f8552fdc84425a8ba70a05d01b_f592140f4edd4a6043a79322e892babb.png)
De cette manière, il leur a été possible de calculer l’énergie d’un atome, en utilisant cette fonctionnelle d’énergie cinétique combinée avec l’expression classique des interactions noyau–électron et électron–électron qui peuvent eux aussi être exprimées en termes de densité électronique.
![E_{TF}[n]=\frac{3}{10}(3\pi^2)^{2/3}\int n^{5/3}(r) d^3r + \int{ V_{ext}(r)n(r)dr} + \frac{1}{2} \int{\frac{n(r)n(r')}{|r-r'|}drdr'}](https://static.techno-science.net/illustration/Definitions/autres/c/c800a2c9c1f7f97a783e9c0010d02f5b_a544658a27127dc468e5c5047e065400.png)
Bien que cela soit une importante première étape, la précision de l’équation de Thomas-Fermi reste cependant limitée, parce que la fonctionnelle de l’énergie cinétique résultante est approximée mais aussi parce que cette méthode ne tient pas compte de l’énergie d’échange d’un atome, conséquence du principe de Pauli, ni de la corrélation électronique. Une fonctionnelle d’échange énergétique fut ajoutée par Paul Dirac en 1930.
Cependant, la méthode de Thomas-Fermi-Dirac reste relativement imprécise pour la plupart des applications, la plus grande source d’erreur provenant de l’écriture de l’énergie cinétique qui peut toutefois être améliorée en y ajoutant la correction proposée en 1935 par Carl von Weizsäcker qui prend en compte le gradient de la densité dans l'expression de la fonctionnelle de l'énergie cinétique :
![T_W[n]=\frac{1}{8}\frac{\hbar^2}{m}\int\frac{|\nabla n(r)|^2}{n(r)}dr](https://static.techno-science.net/illustration/Definitions/autres/6/635a79018ee06cd0c59802c7b933ad76_48e47cda34b5f4872f1e039690328e4b.png)
La methode de Thomas-Fermi a été notamment utilisée pour les équations d'états des éléments chimiques mais sa portée ne peut être guère plus étendue. Edward Teller a en effet montré en 1962 que la théorie de Thomas-Fermi était incapable de decrire la liaison moléculaire.
Une méthode ab initio ou semi-empirique?
Les méthodes basées sur la théorie de la fonctionnelle de la densité sont considérées à l'heure comme une théorie ab initio par la plupart des scientifiques. En effet, les théorèmes de Hohenberg et Khon ainsi que le développement amenant aux équations monoélectroniques de Kohn et Sham sont parfaitement rigoureux et sont obtenus sans avoir recours à d'éventuelles approximations. Cependant, la fonctionnelle d'échange-corrélation apparaissant dans les équations rend toutes résolutions exactes impossibles, sa forme analytique étant inconnue. Comme décrit plus haut, il est donc nécessaire d'approximer cette fonctionnelle soit en formulant une forme mathématique approchée de la fonctionnelle ou bien en fittant un certain nombre de données expérimentales. Cette approche est typique des méthodes semi-empiriques et la méthode DFT pourrait donc tout aussi bien être classée dans cette catégorie. L'énergie totale en DFT est exprimée en termes dépendant de la densité électronique plutôt qu'en termes de fonctions d'onde. Il est sans doute plus pertinent de considérer la méthode DFT comme une classe à part dans les méthodes numériques de chimie quantique.

















































