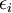Théorie de la fonctionnelle de la densité - Définition
La liste des auteurs de cet article est disponible ici.
Formalisme mathématique
Théorèmes de Hohenberg et Kohn
L'approche développée par Pierre Hohenberg et Walter Kohn est de reformuler la théorie de la fonctionnelle de la densité proposée par Thomas et Fermi par une théorie exacte d'un système à plusieurs corps. La formulation est applicable pour tout système de particules en interaction évoluant dans un potentiel externe et repose sur deux théorèmes essentiels qui furent énoncés et démontré par Hohenberg et Kohn dans leur article de 1964.
|
Le Premier Théorème HK peut se démontrer très simplement en utilisant un raisonnement par l'absurde. Supposons qu'il puisse exister deux potentiels externes différents
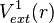
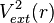
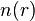
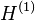
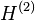
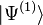
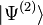
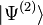
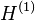
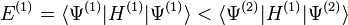
Cette inégalité stricte est valable si l'état fondamental est non dégénéré ce qui est supposé dans le cas de l'approche de HK. Le dernier terme de l'expression précédente peut s'écrire :
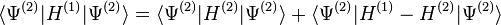
![= E^{(2)}+ \int [V_{ext}^1(r)-V_{ext}^2(r)]n_0(r)d^3r](https://static.techno-science.net/illustration/Definitions/autres/1/18a84239a9168abcf6dc3a12f3291303_bcb6d552f8ad78fbbc60f5510d96b2cb.png)
ce qui donne :
![E^{(1)}< E^{(2)}+ \int [V_{ext}^1(r)-V_{ext}^2(r)]n_0(r)d^3r](https://static.techno-science.net/illustration/Definitions/autres/1/18ccd21ce6437563ae25f7cbc85f4908_8132ce7fa1fe6868338f820946f43c14.png)
Il va également de soi que le même raisonnement peut être réalisé en considérant
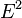
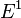
![E^{(2)}< E^{(1)}+ \int [V_{ext}^2(r)-V_{ext}^1(r)]n_0(r)d^3r](https://static.techno-science.net/illustration/Definitions/autres/f/ff5375f459594e68ea6208a4566c8371_1b39bc9ac026338f961c62d90135a179.png)
On additionnant membre à membre ces deux dernières équations, on obtient l'égalité contradictoire suivante :
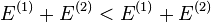
Le schéma ci-dessous illustre l'apport que fournit le premier théorème de Hohenberg et Khom. Les simples flèches indiquent le schéma obtenu dans le cas de la résolution traditionnelle de l'équation de Schrödinger où la connaissance du potentiel externe va permettre de déterminer les différents états électroniques (c'est-à-dire les fonctions d'ondes) ainsi que l'état fondamental et la densité électronique qui lui est associée. Le premier théorème HK, représenté par la double flèche, permet de compléter ce cycle. Cela signifie que toutes les propriétés du système peuvent être complètement déterminées si l'on connait la densité électronique de l'état fondamental.
![\begin{array}[t]{lcl} V_{ext}(r) &\Longleftarrow & n_0(r) \\ \downarrow & & \uparrow \\ \Psi_i({r}) & \rightarrow & \Psi_0({r}) \end{array}](https://static.techno-science.net/illustration/Definitions/autres/9/9ec96542bbe6e1c85d2140cc128be5de_bc517c3175330b3baf9a59d79186fe08.png)
|
Toutes les propriétés du système étant définies par la connaissance de la densité
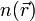
![E_{HK}[n]=T[n]+ U[n]+ \int V_{ext}(\vec r)n(\vec r) d^3r + E_{II}](https://static.techno-science.net/illustration/Definitions/autres/4/47ce660b8d1985ecf51d1c4d258ffe0c_336dfb2f507e815455897f65f8df5411.png)
![= F_{HK}[n]+\int V_{ext}(\vec r)n(\vec r) d^3r + E_{II}](https://static.techno-science.net/illustration/Definitions/autres/4/4a1003e71bc96f5b72e8f2a66c63ee0e_a569d11136e9d929f004583f68c89567.png)
où
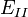
![\,\! F_{HK}[n]](https://static.techno-science.net/illustration/Definitions/autres/c/c5df61846ac602e226d6a35e8fbbcea6_87ecfe15109e4fb6a521885dd643060e.png)
![\,\! F_{HK}[n] = T[n]+ U[n]](https://static.techno-science.net/illustration/Definitions/autres/7/750787b0889c3789eb147cad92dfc02a_f3013c632d5488ed926e4b898ced975c.png)
Considérons à présent un système ayant une densité à l'état fondamental noté
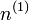
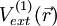
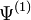
![E^{(1)} = F_{HK}[n^{(1)}] = \langle \Psi^{(1)}|H^{(1)}|\Psi^{(1)}\rangle](https://static.techno-science.net/illustration/Definitions/autres/a/ad18071706508e1530e89a468ece548c_e14970075de4b6645fc046ada6f48ac3.png)
Si nous considérons à présent une densité différente
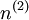
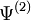
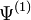
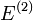
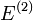
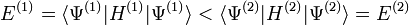
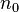
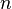
![\,\! F_{HK}[n]](https://static.techno-science.net/illustration/Definitions/autres/c/c5df61846ac602e226d6a35e8fbbcea6_87ecfe15109e4fb6a521885dd643060e.png)
Le second théorème montre que l'énergie apparaît comme une fonctionnelle de la densité, et que pour tout potentiel extérieur, la densité qui minimise cette fonctionnelle est la densité exacte de l'état fondamental.
En conclusion, les deux théorèmes proposés par Hohenberg et Kohn permettent de déplacer le problème posé par la résolution d’une équation de Schrödinger multiélectronique. En effet, la méthode DFT nous enseigne que si la forme de la fonctionnelle est connue, il est relativement aisé, pour un potentiel externe donné, de déterminer l’énergie de l'état fondamental. Le problème qui se pose est alors la formulation de la fonctionnelle
![\,\! F[n]](https://static.techno-science.net/illustration/Definitions/autres/8/84c035108cf511edb68e07f4b3c0c829_e89ff2c14857b57edbbe177b3431094c.png)
![\,\! T[n]](https://static.techno-science.net/illustration/Definitions/autres/2/2220bca035dc1ca4b3c43a0465cf7de4_e29a111dbc1f20ba9e4ef534318636fc.png)
Ansatz de Kohn et Sham
« Si vous n'aimez pas la réponse, modifiez la question. »
—
L’énergie cinétique d’un gaz d’électrons en interaction étant inconnue, Walter Kohn et Lu Sham ont proposé en 1965 un ansatz qui consiste à remplacer le système d'électrons en interaction, impossible à résoudre analytiquement, par un problème d'électrons indépendants évoluant dans un potentiel externe.
Mathématiquement, cela revient à exprimer la fonctionnelle énergie totale de Hohenberg et Kohn décrite comme :
![E_{HK}[n] = F[n] + \int V(r)n(r)dr](https://static.techno-science.net/illustration/Definitions/autres/4/472cb33d0bdcd630ae43055aaaf3c7ce_d2894e565c6759126d4979ec018e0314.png)
par l'expression suivante :
![\,\! E_{S}[n] = T_{S}[n] + V_{S}](https://static.techno-science.net/illustration/Definitions/autres/9/9578633f5d77d53caeaf7dbc2b736670_129768873d0f4433c45e16ef10d1e9f4.png)
où
![\,\! T_{S}[n]](https://static.techno-science.net/illustration/Definitions/autres/f/f147bbb38e56b65ba9f257d99d510a2c_9b00339c970a94e40a3001189fda8250.png)
![\,\! V_{S}[n]](https://static.techno-science.net/illustration/Definitions/autres/8/832fa6ccda8cdadf2eadcd71a1a10de1_47bd13599fc8fd903f61576ebb497709.png)
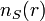
![\,\! V_{S}[n]](https://static.techno-science.net/illustration/Definitions/autres/8/832fa6ccda8cdadf2eadcd71a1a10de1_47bd13599fc8fd903f61576ebb497709.png)
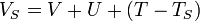
C'est-à-dire si celui-ci inclut la correction à l'énergie cinétique suite à l'ansatz de Khon et Sham. L'intérêt de la reformulation introduite par Khon et Sham est que l'on peut maintenant définir un hamiltonien monoélectronique et écrire les équations de Khon-Sham monoélectroniques qui, contrairement à l'équation de Schrödinger définie plus haut, peuvent être résolues analytiquement.
![\left[-\frac{\hbar^2}{2m}\nabla^2+V_s(\vec r)\right] \phi_i(\vec r) = \epsilon_i \phi_i(\vec r),](https://static.techno-science.net/illustration/Definitions/autres/c/c9a797a1b4d0b830dd45383af75b9142_d66fc0c9b39c7c964bbcf8fa45f16d40.png)
La résolution des équations de Khon-Sham va permettre de déterminer les orbitales
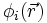
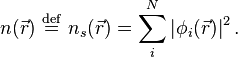
Le potentiel effectif monoélectronique apparaissant dans l'équation peut être exprimé de manière plus détaillée comme :
![V_s = V + \int \frac{n_s(\vec r\,) n_s(\vec r\,')}{|\vec r-\vec r\,'|} {\rm d}^3r' + V_{\rm XC}[n_s(\vec r)]](https://static.techno-science.net/illustration/Definitions/autres/c/c589775595ba81530854a16e9bc4cd61_ad2a748bb14190dd3f1628894871412b.png)
Le premier terme est le potentiel externe créé par les noyaux, le deuxième exprime l'interaction coulombienne classique entre paire d'électrons (et est également appelé potentiel Hartree). Le dernier terme est le potentiel d'échange-corrélation et contient, outre l'échange et la corrélation électronique, les corrections à l'énergie cinétique. Celle-ci n'est pas connue exactement, le choix d'une fonction d'échange corrélation approximée constitue l'un des principaux choix d'approximation en DFT dans l'approche Kohn-Sham .
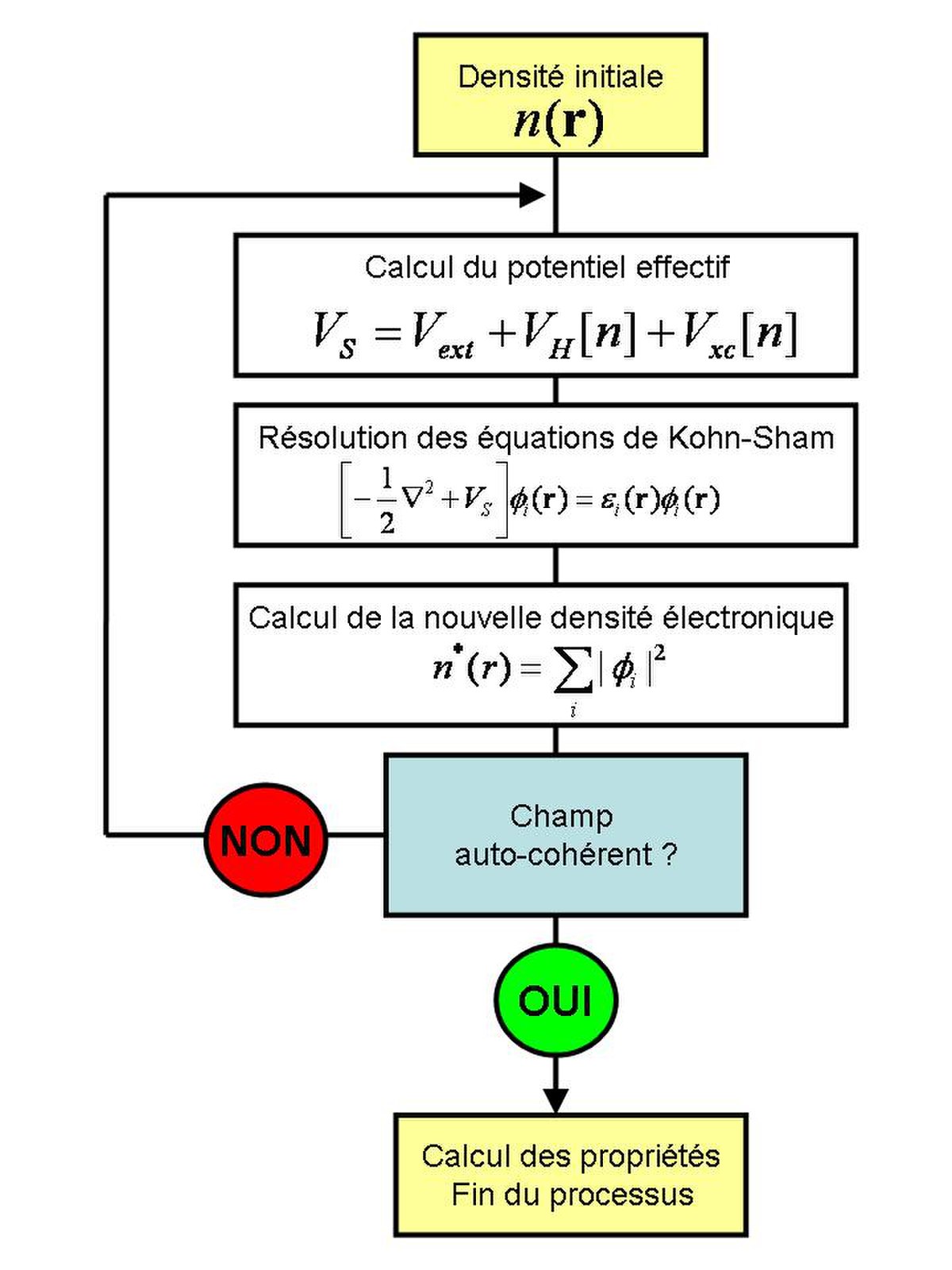
Comme on peut l'observer dans l'équation, ce potentiel dépend de la densité électronique, qui elle-même est calculée à partir des fonctions d'ondes des électrons indépendants, qui elle-même dépend du potentiel calculé à partir de la densité , etc. Cette approche conduit donc à un traitement dit self-consistent field (ou méthode du champ auto-cohérent): en partant d'une valeur arbitraire de départ, on calcule en boucle les valeurs de densité, potentiel et fonctions d'ondes jusqu'à une situation stable où ces différentes valeurs n'évoluent presque plus.
Résolution numérique des équations de K-S
L'ansatz de Kohn et Sham permet d'aboutir à un ensemble d'équations de Schrödinger monoélectroniques connues sous le nom d'équations de Kohn-Sham :
![\Big[ - \frac{\nabla^2}{2m} + V_{ext} + V_H + V_{xc} \Big]\phi_i = \epsilon_i \phi_i](https://static.techno-science.net/illustration/Definitions/autres/c/cdcae6cd76b92bd02b3bcfde7f4f76dc_cb27c96b869ac525d67a1590d55e816c.png)
qui doivent être résolues numériquement selon un processus itératif. De manière à pouvoir résoudre ces équations de manière numérique, un certain nombre d'approximations peuvent ou doivent être envisagées. Klaus Capelle recense ainsi trois types d'approximations qui peuvent globalement être distinguées en DFT. L'une est purement conceptuelle et concerne l'interprétation à donner aux valeurs propres