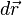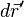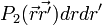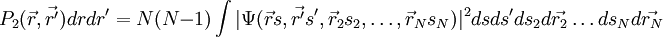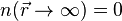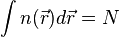Théorie de la fonctionnelle de la densité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Méthodes numériques pour le calcul de la structure électronique |
| Hartree-Fock |
| Théorie de la perturbation de Møller-Plesset |
| Interaction de configuration |
| Méthode du cluster couplé |
| Champ multi-configurationnel auto-cohérent |
| Théorie de la perturbation multi-référence |
| Théorie de la fonctionnelle de la densité |
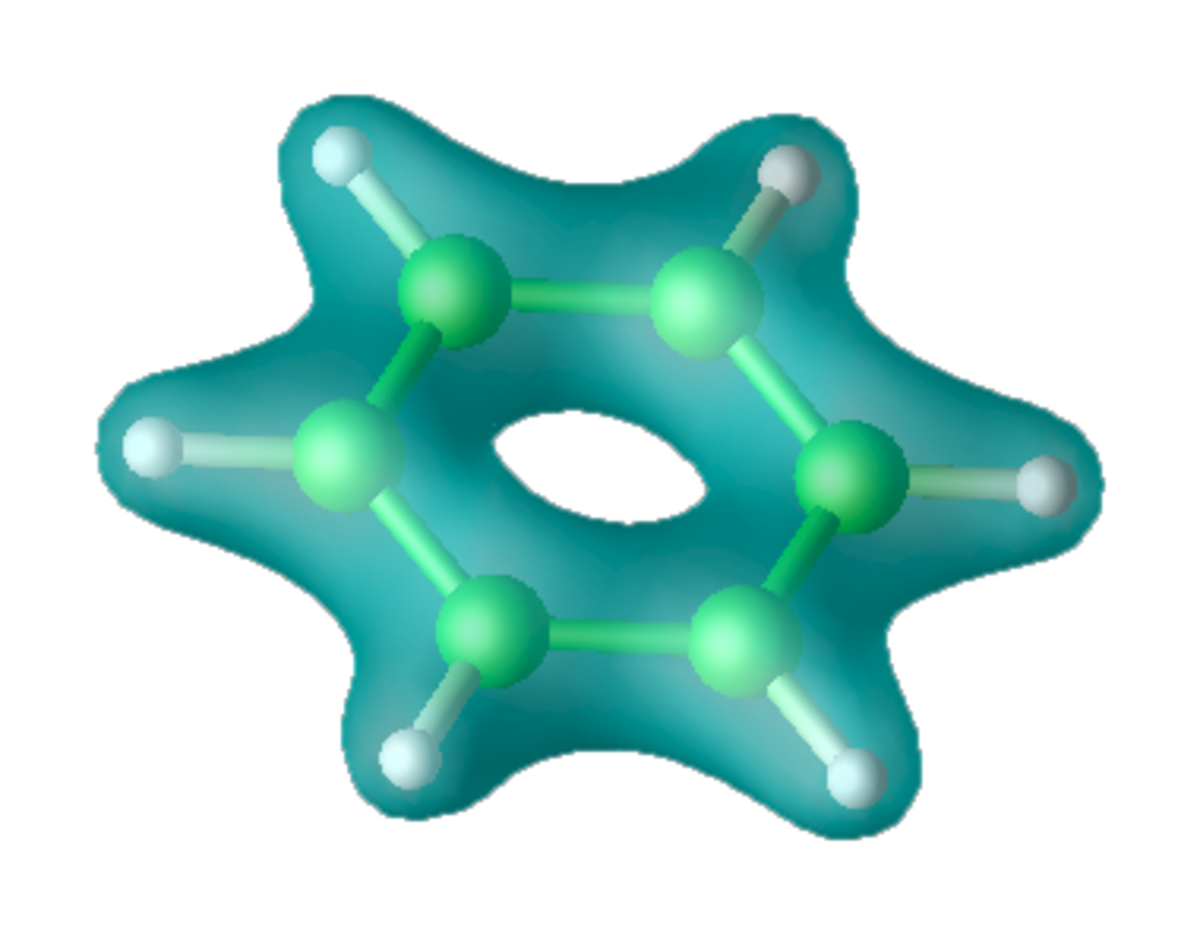
La théorie de la fonctionnelle de la densité (pour Density Functional Theory, sous-entendu électronique : DFT) constitue au début du XXIe siècle l'une des méthodes les plus utilisées dans les calculs quantiques de la structure électronique de la matière (atomes, molécules, solides) aussi bien en physique de la matière condensée qu'en chimie quantique. La DFT trouve ses origines dans le modèle développé par Llewellyn Thomas et Enrico Fermi à la fin des années 1920. Néanmoins il faudra attendre le milieu des années 1960 et les contributions de Pierre Hohenberg, Walter Kohn et Lu Sham pour que soit établi le formalisme théorique sur lequel repose la méthode actuelle.
Les méthodes traditionnelles dans les théories de la structure électronique de la matière, en particulier la théorie Hartree-Fock et les méthodes dérivées de ce formalisme, se fondent sur une fonction d'onde multiélectronique. L'objectif principal de la théorie de la fonctionnelle de la densité est de remplacer la fonction d'onde multiélectronique par la densité électronique en tant que quantité de base pour les calculs. Alors que la fonction d'onde multiélectronique dépend de 3N variables (où N est le nombre total de particules du système), la densité est seulement fonction de trois variables ; il s'agit donc d'une quantité plus facile à traiter tant mathématiquement que conceptuellement. Le principe de la DFT consiste en une reformulation du problème quantique à N corps en un problème monocorps (ou, à la rigueur, bi-corps si l'on considère les problèmes de spin) avec pour paramètre la densité électronique. L'idée centrale de la DFT est que la seule densité électronique de l'état fondamental du système détermine entièrement les valeurs moyennes des observables, comme par exemple l'énergie.
La DFT a été à l'origine principalement développée dans le cadre de la théorie quantique non-relativiste (équation de Schrödinger indépendante du temps) et dans l'approximation de Born-Oppenheimer. La théorie fut par la suite étendue au domaine de la mécanique quantique dépendante du temps (on parle alors de TDDFT pour Time-Dependent Density Functional Theory) et au domaine relativiste. La DFT est également utilisée pour la description thermodynamique des fluides classiques.
Notions de base
« Les lois physiques fondamentales nécessaires à la théorie mathématique d'une grande partie de la physique et de la totalité de la chimie sont ainsi complètement connues, et la difficulté est seulement que l'application exacte de ces lois mène à des équations beaucoup trop complexes pour être résolues »
— Paul A.M. Dirac, 1929
Equation de Schrödinger
L'équation fondamentale à résoudre pour décrire la structure électronique d'un système à plusieurs noyaux et électrons est l'équation établie par Erwin Schrödinger en 1925, appelée depuis équation de Schrödinger, et qui s'écrit :
![H\Psi = \left[- \sum_i^N \frac{\hbar^2}{2m}\nabla_i^2 - \sum_{I}^A \frac{\hbar^2}{2M}\nabla_I^2 - \sum_{i,I} \frac{Z_I e^2}{|\vec r_i - \vec R_I|} + \sum_{i<j} \frac{e^2}{|\vec r_i - \vec r_j|} + \sum_{I<J} \frac{Z_I Z_J e^2}{|\vec R_I - \vec R_J|}\right] \Psi= E\Psi](https://static.techno-science.net/illustration/Definitions/autres/6/6ea755aaaf57600a6b339c2dca3f1f9b_1659705d75c1eba278227fad1ce83be7.png)
où
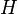
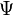
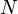
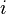
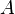
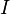
Sous cette forme, l'équation de Schrödinger est trop complexe pour pouvoir être résolue analytiquement. De manière à simplifier la résolution de cette équation, Max Born et Robert Oppenheimer ont proposé une approximation visant à simplifier l'équation de Schrödinger. L'approximation de Born-Oppenheimer considère la position des noyaux atomiques comme fixes ; leur énergie cinétique peut donc être négligée et le terme d'interaction entre noyaux considéré comme une constante (que l'on notera
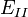
![H\Psi = \left[- \sum_i^N \frac{\hbar^2}{2m}\nabla_i^2 - \sum_{i,I} \frac{Z_I e^2}{|\vec r_i - \vec R_I|} + \sum_{i<j} \frac{e^2}{|\vec r_i - \vec r_j|} + E_{II}\right] \Psi= E\Psi](https://static.techno-science.net/illustration/Definitions/autres/0/0e8e7cec41d7c2a18517a7b09af95a3a_0eb0433cdafc23e92ec7ebb61102ced9.png)
De manière à alléger les notations, on représentera, par convention, l'opérateur énergie cinétique par
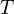
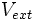
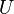
![\,\! H\Psi = [T + V_{ext} + U]\Psi = E\Psi](https://static.techno-science.net/illustration/Definitions/autres/f/fb608fc81b50578bf864736cee1bbd1d_e0408702aa77ca9cfb7c7e585cc20fc0.png)
De nombreuses méthodes ont été développées pour résoudre l'équation de Schrödinger multiélectronique en décrivant par exemple la fonction d'onde comme un déterminant de Slater; c'est le cas de la méthode Hartree-Fock. La DFT fournit une méthode alternative en considérant comme quantité de base pour la description du système la densité électronique.
Densité électronique
Définition et propriétés
La probabilité de trouver un électron parmi les
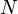
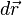
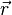
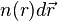
où
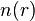
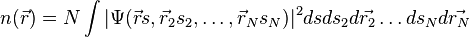
La densité de probabilité possède notamment deux propriétés importantes :
Densité de paire
La densité de paire est la probabilité de trouver simultanément 2 des N électrons du système dans les éléments de volume