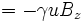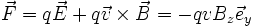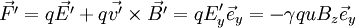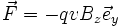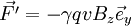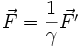Transformations de Lorentz du champ électromagnétique - Définition

Applications

Électron dans un champ magnétique uniforme (mécanique relativiste)

Description du problème

Le problème est le même que celui décrit plus haut mais on se place maintenant dans le contexte de la relativité restreinte.

Calcul des forces

Par rapport au cas étudié dans le cas de la relativité galiléenne, on constate que l'expression du champ électrique dans le référentiel lié à l'électron donne :

Dans le référentiel du laboratoire, on a :

Dans le référentiel lié à l'électron, on a :

En notant que :

, la vitesse de l'électron mesurée dans le référentiel du laboratoire n'est rien d'autre que :

, la vitesse du référentiel lié à l'électron par rapport au référentiel du laboratoire, on trouve :

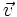
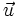
Ou encore :

Ce qui est le résultat attendu.

Analyse

Bien que l'expression finale de la force n'est pas la même suivant le référentiel, ce qui donnerait en mécanique newtonienne une description du mouvement de l'électron différente suivant le référentiel et serait inacceptable, c'est le résultat attendu en mécanique relativiste.
En effet, en dynamique relativiste, le rapport entre l'expression finale de la composante d'une force perpendiculaire au mouvement entre 2 référentiels galiléens doit être dans un rapport pour que la description du mouvement soit semblable (ou cohérente) dans les 2 référentiels.
Dans le référentiel lié à l'électron, il est également nécessaire d'expliquer la présence d'un champ électrique.

2 électrons en déplacement parallèle (mécanique relativiste)

Description du problème

Champs et forces dans le référentiel lié aux électrons

Champs et forces dans le référentiel du laboratoire

A partir des transformations de Lorentz

A partir des équations de Maxwell

Analyse

Champ électrique autour d'un électron en mouvement

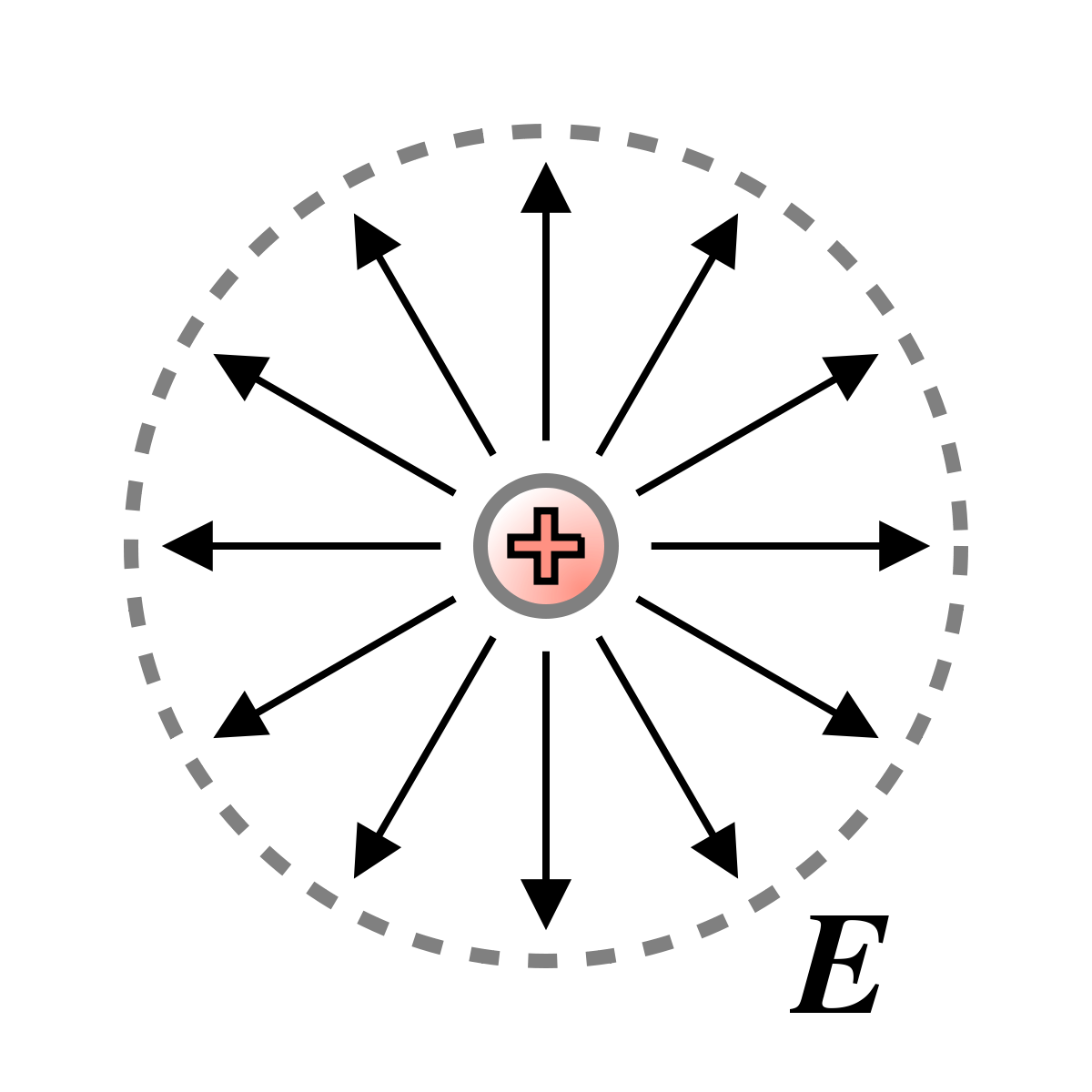
Une particule chargée, au repos dans le vide, engendre un champ électrique isotrope, identique dans toutes les directions de l'espace.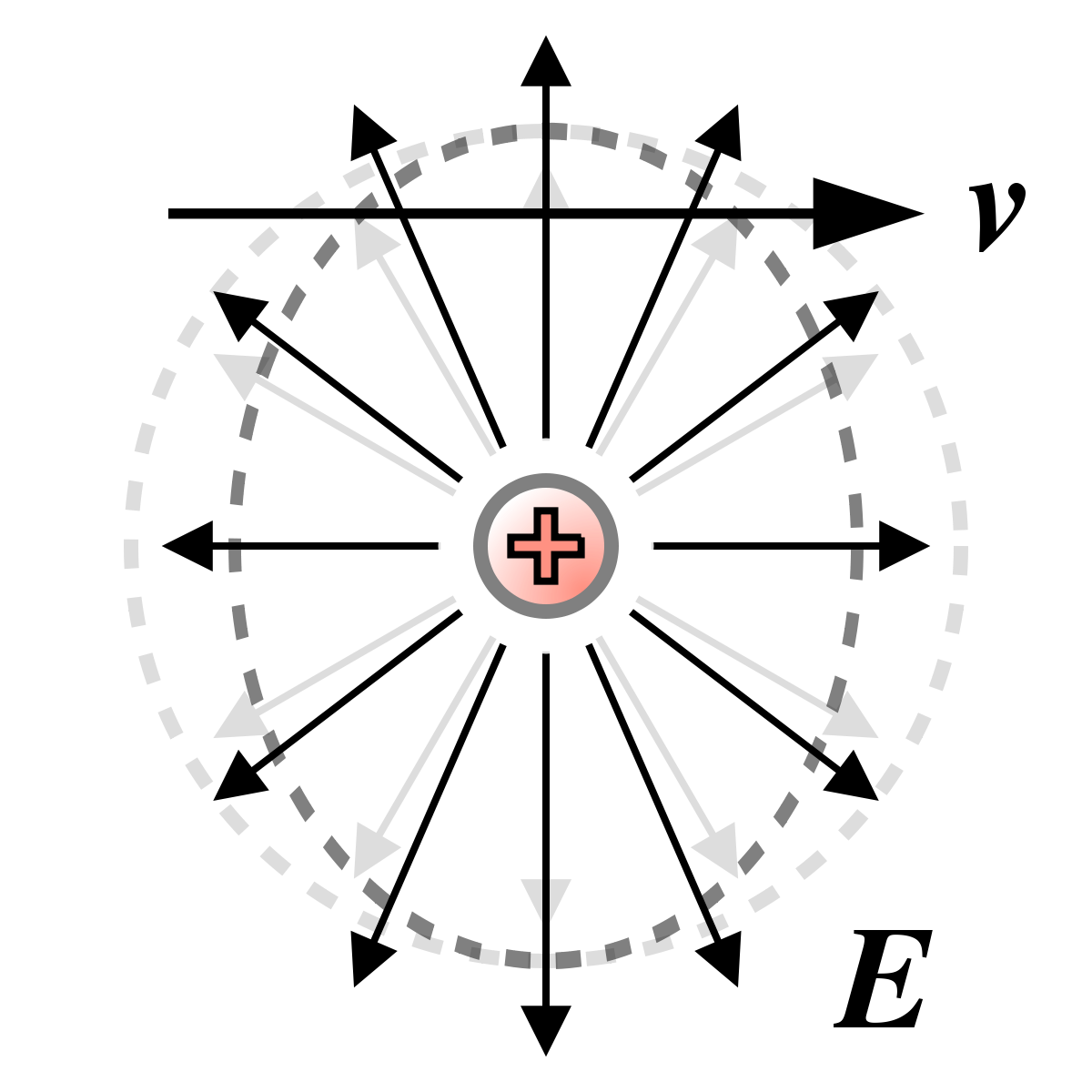

En revanche, son déplacement brise cette symétrie, à cause d'effets relativistes : cette déformation est à l'origine du champ magnétique.

Description du problème

Champs et forces dans le référentiel lié aux électrons

Champs et forces dans le référentiel du laboratoire

A partir des transformations de Lorentz

A partir des équations de Maxwell

Analyse

Électron dans le voisinage d'un fil parcouru par un courant

Voir article détaillé : Electron au voisinage d'un fil parcouru par un courant