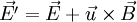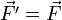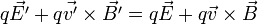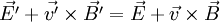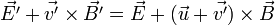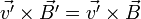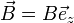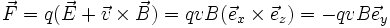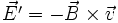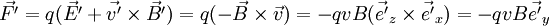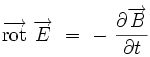Transformations de Lorentz du champ électromagnétique - Définition
La liste des auteurs de cet article est disponible ici.
Approximation galiléenne
Soit :
- un référentiel

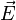
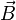
- un référentiel



-



On a :
Puisque
-
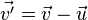
Il faut que :
Autrement dit, il faut que :
Autrement dit, il faut que :
Autrement dit, il faut que :
Aucun champ ne dépendant de , on peut prendre par exemple , donc il faut que :
Par soustraction des deux lignes précédentes, on a :
ce qui donne :
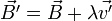
Aucun champ ne dépendant de , on peut considérer deux non colinéaires et ainsi s'apercevoir que la seule valeur correspondante est , donc il faut que :
Au final, cela donne :
Application : électron dans un champ magnétique (mécanique newtonienne)
Description du problème
Considérons un électron se déplaçant avec une vitesse v dirigée suivant x dans une zone où existe un champ d'induction magnétique vertical uniforme :
et cherchons à déterminer la force électromagnétique appliquée sur lui respectivement dans le référentiel du laboratoire et dans un référentiel qui lui est lié.
Calcul des forces
Dans le référentiel du laboratoire,
l'électrons est animé d'une vitesse
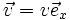
Il subit une force :
Dans un référentiel lié à l'électron, on a :
-
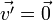
Suivant le principe des transformations de Lorentz, un observateur mesure dans ce référentiel un champ électrique tel que :
On en déduit que l'électron subit une force :
On constate que :
-
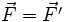
Le principe d'invariance galiléenne est respecté.
Analyse
Dans le référentiel du laboratoire la situation est traditionnelle. Elle correspond au déplacement d'une charge devant un aimant.
Dans la référentiel de l'électron, l'observateur considère ce dernier fixe et voit un aimant se déplacer devant lui dans la direction .
L'origine du champ magnétique est évidente. Il est dû à l'aimant. On peut déduire le champ électrique à partir des transformations de Lorentz du champ EM.
Toutefois, étant donné que les lois de la physique sont covariantes par transformation de référentiel galiléen, l'origine du champ électrique créé par l'aimant doit se déduire des lois physiques qui permettent de déterminer les champs EM cad des équations de Maxwell appliquées à la configuration étudiée.
En particulier, on peut se demander qu'elle est l'origine du champ électrique qui ne peut être généré que par la translation de l'aimant.
Dans le cas présent, on peut déduire la valeur du champ par application de l'équation de Maxwell-Faraday
intégrée sur un rectangle dont un côté comprend la tige et un autre côté est parallèle à la tige dans une zone où le champ d'induction magnétique est nul.
Limites du modèle
Toutefois de manière générale, les équations de Maxwell ne sont pas covariantes par transformation galiléenne.
Pour une compréhension globale, il faut souligner que l'électromagnétisme "classique", c'est-à-dire étudié dans le cadre de la mécanique newtonienne mène à des paradoxes qui montrent les limites du modèle et qui ont amené Einstein à introduire la mécanique relativiste. Le développement de la mécanique relativiste a permis à son tour de simplifier le modèle de Maxwell. On a démontré depuis que l'ensemble des équations de Maxwell pouvaient être démontré à partir de la seule loi de Coulomb dans le cadre de la mécanique relativiste. Une illustration est donnée par l'exemple d'un électron dans le voisinage d'un fil parcouru par un courant traité dans le modèle relativiste.