Transformations de Lorentz du champ électromagnétique - Définition

Introduction

Les transformations de Lorentz du champ électromagnétique permettent de déterminer ce que devient le couple champs électrique - magnétique :

quand on passe d'un référentiel inertiel à un autre sans avoir à résoudre (à nouveau) les équations de Maxwell pour les déterminer.

Introduction

Les mesures réalisées par un observateur dépendent du référentiel depuis lequel elles sont réalisées. Par exemple, la vitesse d'un corps varie suivant le référentiel dans lequel on la mesure : la vitesse d'un bateau mesurée par rapport à la berge est différente de celle mesurée par rapport à l'eau du fleuve dans lequel il se déplace.

Certaines grandeurs sont indépendantes du référentiel dans lequel on les mesure. Par exemple, quand on passe d'un référentiel galiléen à un autre référentiel galiléen, l'accélération est une grandeur dont la mesure est conservée.

Les lois de Newton sont telles que la mesure d'une force doit être invariante d'un référentiel galiléen à un autre. En mécanique classique (ou newtonienne), on dit que les lois physiques doivent être covariantes par transformation galiléenne. En d'autres mots, il faut que les forces qu'on peut déduire de ces lois aient la même expression dans tout référentiel galiléen.

Suivant ce principe, l'expression de la force électromagnétique :

est donc invariante suite à ce passage de référentiel.

Étant donné que l'expression fait intervenir la vitesse , qui n'est pas invariante mais que l'expression de la force doit rester invariante, on en déduit que :

et ne peuvent être invariants.

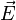
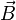
En conséquence, la valeur qu'un observateur doit donner aux champs électrique et magnétique dépend du référentiel galiléen où ils sont mesurés.

Cas relativiste

Introduction

En mécanique classique, les équations de Maxwell auxquelles on rajoute l'équation de la force de Lorentz devraient donc être covariantes par transformations de référentiel galiléen.

Elles ne le sont pas.

Cela signifie que l'expression des équations de Maxwell n'est pas conservée quand on leur applique une transformation galiléenne. Les équations (de Maxwell) à appliquer pour déterminer les champs EM qu'on utilise dans la force de Lorentz devraient donc changer suivant le référentiel galiléen où on les utilise.

En d'autres termes, si on ne change pas l'expression des équations de Maxwell qu'on utilise quand on change de référentiel galiléen (ce qui est le cas en mécanique rélativiste), les champs EM qu'on en déduit ne donnent pas la même expression finale pour la force de Lorentz et donc les mouvements qu'on peut en déduire (en mécanique newtonienne) pour les particules chargées ne sont plus les mêmes.

Le fait que la description du mouvement change selon le référentiel n'est pas acceptable. Le fait que l'expression de lois physiques change quand on passe d'un référentiel galiléen à un autre est problématique car la relativité galiléenne suppose que tous les référentiels galiléens sont équivalents.

La non covariance des équations de Maxwell par transformation galiléenne et la nécessité d'avoir une description du mouvement cohérente dans tout référentiel a donc amené les chercheurs de l'époque à postuler l'existence d'un référentiel privilégié (ou particulier) où les équations de Maxwell auraient eu la forme qu'on leur connait mais qu'il aurait fallu "corriger" pour les appliquer dans d'autres référentiels. L'idée est similaire à la correction de la loi de Newton que l'on effectue en rajoutant la force centrifuge quand on travaille dans un référentiel non inertiel si ce n'est qu'ici, la correction devrait être apportée même entre référentiels inertiels.

C'est dans ce contexte de la recherche du référentiel inertiel privilégié qu'eurent lieu les expériences sur l'éther.

Transformations de Lorentz

Voir article principal : Transformations de Lorentz

Toujours dans ce contexte mais dans une approche plus théorique, Lorentz a trouvé à l'époque des transformations qui rendaient les équations de Maxwell et la force de Lorentz covariantes. A cette époque, c'était d'un intérêt purement mathématique puisque les lois de la mécanique (les lois de Newton) sont covariantes par transformation galiléenne, pas par transformations de Lorentz. De plus ces dernières n'avaient aucun sens physique particulier.

Transformations de Lorentz du champ électromagnétique

Soit :

un référentiel dans lequel on mesure et

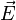
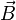
un référentiel dans lequel on mesure et

, la vitesse de mesurée dans .

En notant :

avec la vitesse de la lumière dans le vide.

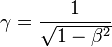
On a :

Pour des vitesses non relativistes ( ), on retrouve les équations données plus haut dans l'approximation galiléenne.

Lien avec la mécanique relativiste (A. Einstein)

Einstein a donné leur sens aux transformations de Lorentz quand il a écrit son article On the Electrodynamics of moving bodies reformulant les lois de la dynamique et qu'il a découvert le principe de la relativité de l'espace et des durées.

Dans le paragraphe 6, il exprime que la force magnétique qui agit sur un électron n'est qu'un effet relativiste de la force électrique qui agit sur l'électron vu depuis le référentiel au repos avec lui. Il fait le lien entre forces et champs via les transformations de Lorentz des champs électromagnétiques :

"If a unit electric point charge is in motion in an electromagnetic field, the force acting upon it is equal to the electric force which is present at the locality of the charge, and which we ascertain by transformation of the field to a system of co-ordinates at rest relatively to the electrical charge. (New manner of expression.)"

"Si une particule ponctuelle de charge électrique unité est en mouvement dans un champ électromagnétique, la force s'exerçant dessus est égale à la force électrique qui est présente au voisinage de la charge, et que [la force électrique] nous déterminons par transformation du champ dans un système de coordonnées au repos relativement à la charge électrique (nouvelle forme d'expression)"