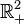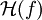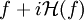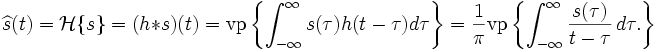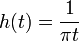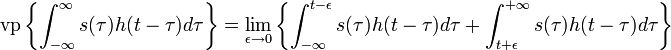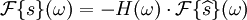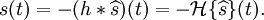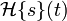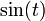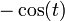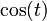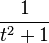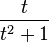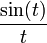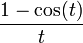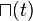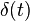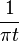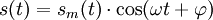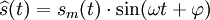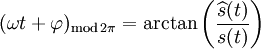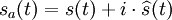Transformée de Hilbert - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et en théorie du signal, la transformée de Hilbert, ici noté

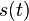
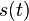
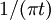
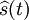
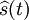
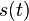
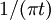
La transformée de Hilbert tient son nom du mathématicien David Hilbert.
Définition
Voici la définition exacte de la transformée de Hilbert :
où
et
vp étant l'abréviation de valeur principale de Cauchy.
On peut montrer que si
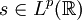
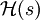
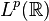

Réponse fréquentielle
Il s'ensuit que la transformation de Hilbert d'un signal fréquentiel donné par la transformée de Fourier :
-
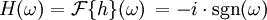
où
-
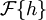
- i (parfois noté j ) le nombre imaginaire,
-
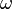
 qui est souvent appelé fonction de signe.
qui est souvent appelé fonction de signe.
Ainsi :
-
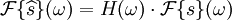
La transformée de Hilbert a pour effet de tourner de +90° la composante de fréquence négative de
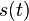
Transformée de Hilbert inverse
On peut remarquer que
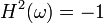
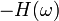
où la transformée de Hilbert inverse apparait clairement :
Considérations pratiques
La fonction h avec h(t) = 1/(π t) est un filtre non causal et donc ne peut pas être faite telle quelle, si s est un signal dépendant du temps. Si s est une fonction à variable non temporelle, par exemple des variables spatiales, la non-causalité ne doit pas être un problème. Le filtre est de plus à support non borné, ce qui peut être un problème dans certaines applications. Un autre problème peut apparaître du fait du comportement à fréquence nulle, ce qui peut être évité en s'assurant que s ne contient pas de composante continue.
Une implémentation pratique implique dans de nombreux cas qu'un filtre à support fini, qui peut de plus être rendu causal grâce à un délai raisonnable, est utilisé pour approximer une simulation informatique. Cette approximation peut aussi impliquer que seule une plage de fréquence spécifique est sujette au changement de phase dû à la transformation de Hilbert.
Exemples de transformées de Hilbert
- Remarque : Certains auteurs, par exemple Bracewell, utilisent notre
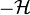
| Signal | transformée de Hilbert |
|---|---|
|
|
|
|
|
|
|
|
|
| Sinus cardinal |
|
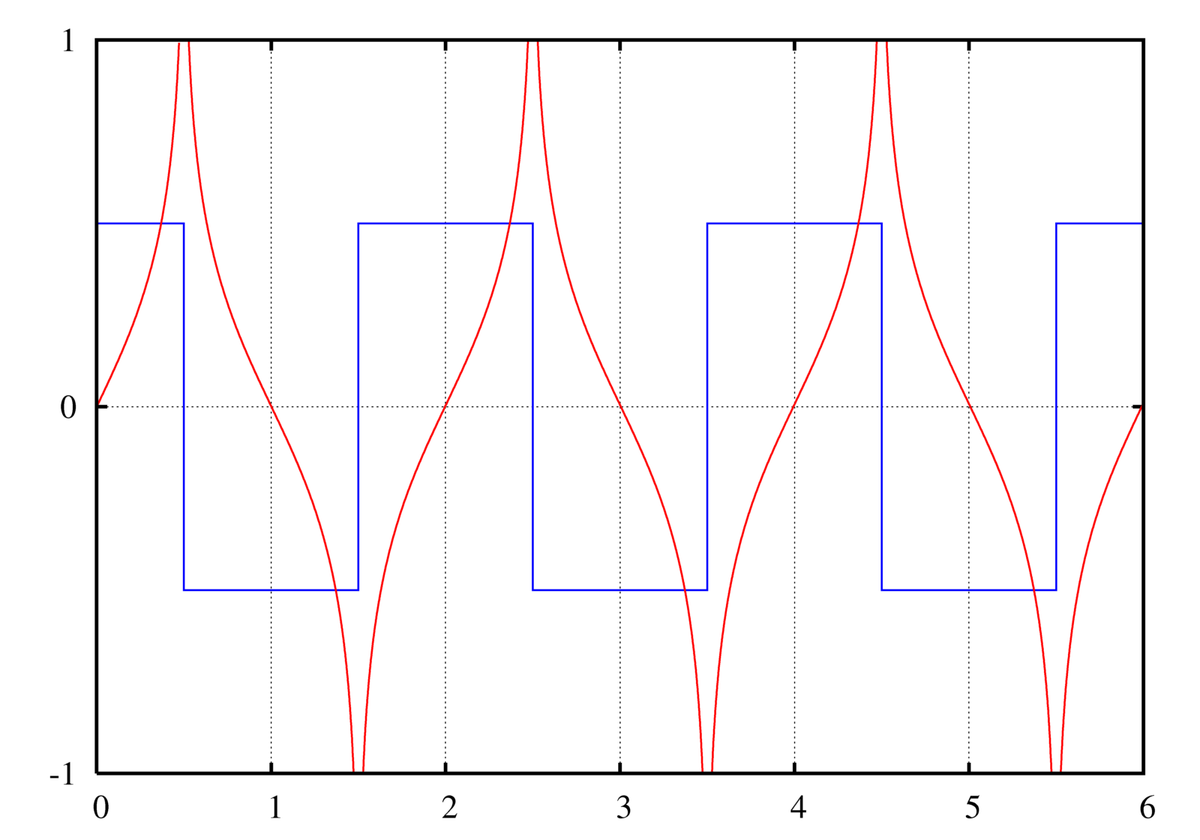
| fonction porte |
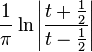
|
| impulsion de Dirac |
|
Modèle à bande étroite
De nombreux signaux peuvent être modélisés par le produit d'un signal harmonique à support borné,
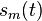
Lorsque
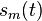
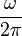
Donc, la transformée de Hilbert peut être simplement vue comme un circuit qui produit un déphasage de 90° de la fréquence de la porteuse. De plus :
d'où on peut reconstruire la porteuse. Puis le message peut être extrait de
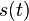
Représentation analytique
Une représentation analytique d'un signal est définie ainsi à l'aide de la transformée de Hilbert :
Par exemple pour le modèle à bandes étroites, la représentation analytique est :
-
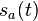
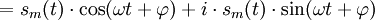
![= s_m(t) \cdot \left[\cos(\omega t + \varphi) + i\cdot \sin(\omega t + \varphi)\right]\,](https://static.techno-science.net/illustration/Definitions/autres/c/c7ea21f15d9691da4bbe1d8b67d095c1_6578fcf008527e2eaa1b40ed7b2ec09b.png)
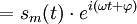
Cette opération complexe hétérodyne enlève les composantes de fréquence négative de
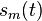
Alors que la représentation analytique d'un signal n'est pas nécessairement analytique, il existe un lien avec les fonctions analytiques, qui est en fait la façon dont la transformée de Hibert est apparue historiquement. L'idée est la suivante. Commençons avec une fonction
on peut l'étendre à une fonction harmonique sur