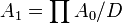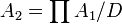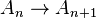Ultraproduit - Définition

Exemples et applications

Les nombres hyperréels sont l'ultraproduit d'une famille dénombrable de copies de R (l'ensemble des nombres réels), pour un ultrafiltre non trivial sur l'ensemble des entiers. L'ordre est une extension de celui de R, ainsi, la suite ω donnée par ω_i = i définit une classe d'équivalence (un nombre hyperréel noté encore ω) plus grand que tout réel (un "infiniment grand"), et la suite ε donnée par ε_i = 1 / i (pour , et ε₀ = 0) définit une classe d'équivalence égale à 1/ω, positive, et plus petite que tout réel (un "infiniment petit"). De façon analogue, on peut construire des entiers ou des complexes non-standards, en prenant une ultrapuissance des ensembles correspondants.

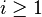
Dans l'étude des grands cardinaux, une construction fréquente consiste à prendre un ultraproduit de tout l'univers (un modèle de la théorie des ensembles) par rapport à un ultrafiltre U bien choisi. Les propriétés de U ont une grande influence sur les propriétés (d'ordre supérieur) de l'ultraproduit ; par exemple, si U est σ-complet, l'ultraproduit sera bien-fondé (si l'univers l'était). Voir cardinal mesurable pour l'exemple de référence.

Parmi les applications les plus frappantes des ultraproduits figurent des preuves très élégantes du théorème de compacité et du théorème de complétude, le théorème de Keisler, qui donne une caractérisation algébrique de la notion sémantique d'équivalence élémentaire, et la présentation (par Robinson et Zakon) de l'utilisation de superstructures et de leurs monomorphismes pour construire des modèles non standards, amenant à la construction, par Abraham Robinson, d'une version de l'analyse non-standard fondée sur le théorème de compacité.

Ultralimites

Ce terme s'emploie surtout pour un ultraproduit d'une suite d'espaces métriques ; pour cette signification, voir l'article détaillé Ultralimite.

En théorie des modèles, une ultralimite (ou ultraproduit limitant) est une limite inductive d'une suite d'ultrapuissances : partant d'une structure, A₀, et d'un ultrafiltre, D₀, on forme l'ultrapuissance , puis on recommence pour former , etc. Pour chaque n, il y a une injection canonique (diagonale) . On peut continuer transfiniment en prenant la limite inductive des étapes précédant les ordinaux limites.