Ultraproduit - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, un ultraproduit est une construction utilisée principalement en algèbre abstraite et en théorie des modèles (une branche de la logique mathématique) ; elle permet par exemple d'obtenir des extensions des réels, les nombres hyperréels, ayant les mêmes propriétés que ceux-ci.
Définition
La méthode générale de construction d'ultraproduits part d'un ensemble d'indices I, d'une structure Mi pour chaque élément i de I (toutes ayant la même signature), et d'un ultrafiltre U sur I. Le choix usuel est de prendre I infini et U non-trivial, c'est-à-dire ne contenant aucune partie finie de I (sinon, l'ultraproduit est isomorphe à l'un de ses facteurs).
Les opérations algébriques sur le produit cartésien
sont définies de la manière habituelle (par exemple, pour une opération (binaire) +, (a + b) i = ai + bi ), et on définit une relation d'équivalence compatible avec les opérations par a ~ b si et seulement si
Alors, l'ultraproduit de cette famille (par rapport à U) est l'ensemble quotient du produit cartésien pour cette relation d'équivalence, muni de la structure quotient (c'est-à-dire que ses éléments sont les classes d'équivalence du produit). C'est pourquoi on le note parfois
On peut définir une mesure m (finiment additive) sur l'ensemble des indices en posant m(A) = 1 si A ∈ U et m(A)= 0 sinon. Alors deux éléments du produit cartésien sont équivalents s'ils sont égaux presque partout sur l'ensemble des indices.
Outre les opérations algébriques, les relations peuvent être étendues de la même manière : R([a1],…,[an]) si et seulement si
où [a] désigne la classe d'équivalence de a pour la relation ~. Par exemple, si tous les Mi sont des corps ordonnés, il en est de même de l'ultraproduit.
Une ultrapuissance est un ultraproduit pour lequel tous les facteurs Mi sont égaux :
Plus généralement, la construction précédente peut encore être effectuée si U est seulement un filtre sur X ; la structure résultante
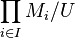
Le théorème de Łoś
Le théorème de Łoś, parfois appelé théorème fondamental des ultraproduits, est dû à Jerzy Łoś (prononcer ˈwɔɕ, approximativement ouosh). Il affirme que toute formule du premier ordre est vraie dans l'ultraproduit si et seulement si l'ensemble des indices i tels que la formule soit vraie dans Mi est un élément de U. Plus précisément :
Soit σ une signature, U un ultrafiltre sur un ensemble I, et pour chaque
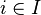
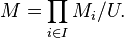
Alors, pour tout
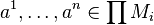
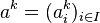
![M \models \phi[[a^1], \ldots, [a^n]]](https://static.techno-science.net/illustration/Definitions/autres/e/e55f43877bdfd89fc67763cb513a26fa_3044f91989ae193c5ed3bd721c0d615d.png)
Le théorème se démontre par récurrence sur la complexité de la formule φ. Le fait que U soit un ultrafiltre (et pas seulement un filtre) est utilisé pour traiter le cas des négations, et l'axiome de choix est nécessaire pour celui de l'introduction d'un quantificateur existentiel.
Exemples
Soit R une relation unaire de la structure M, et *M un ultraproduit de M. Alors l'ensemble
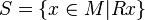
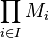
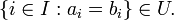
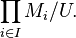
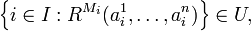
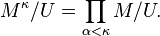
![\{ i \in I : M_{i} \models \phi[a^1_{i}, \ldots, a^n_{i} ] \} \in U.](https://static.techno-science.net/illustration/Definitions/autres/0/0e8e08b938deed5d5689e70669d707ac_ff9b236968d5293b7719a7d8bf2b6243.png)

















































