Ultralimite - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une ultralimite est une construction géométrique qui associe à une suite d'espaces métriques Xn un espace métrique qui est leur "limite". Cette construction est une généralisation de la convergence au sens de Hausdorff, et utilise un ultrafiltre pour éviter d'avoir à considérer des sous-suites convergentes.
Pour la limite inductive d'une suite d'ultraproduits, voir Ultraproduit.
Ultrafiltres
Rappelons qu'un ultrafiltre ω sur l'ensemble des entiers

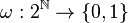
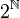

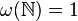

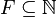
Ultralimite d'espaces métriques pointés
Soit ω un ultrafiltre (non trivial) sur

On dira qu'une suite
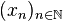
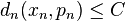
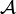
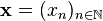
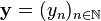
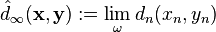
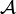
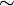
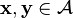
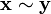
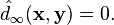
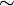
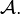
L'ultralimite de la suite (Xn,dn, pn) relativement à ω est un espace métrique
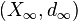
-
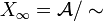
- Pour deux classes d'équivalence (relativement à
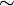
![[\mathbf x], [\mathbf y]](https://static.techno-science.net/illustration/Definitions/autres/f/f4beff4ac68ceee56725ed1aa5432bff_6cde56d024bf7af4760f08398578c48b.png)
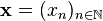
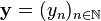
-
![d_\infty([\mathbf x], [\mathbf y]):=\hat d_\infty(\mathbf x,\mathbf y)=\lim_\omega d_n(x_n,y_n).](https://static.techno-science.net/illustration/Definitions/autres/3/3a5a4b0cf11a7bb64c7c435a47932946_6a4e9896e24dd56e36f5665a2aa4e2d8.png)
Il n'est pas difficile de voir que
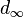
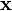

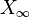
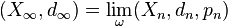
Le cas des espaces uniformément bornés
Supposons que (Xn,dn) soit une suite d'espaces métriques de diamètre uniformément bornés, c'est-à-dire qu'il existe un nombre réel C>0 tel que diam(Xn)≤C pour tout
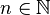
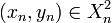
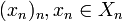
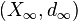
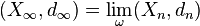
Limite d'une suite relativement à un ultrafiltre
Soit ω un ultrafiltre non-trivial sur

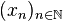
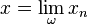
Les propriétés suivantes sont faciles à démontrer :
- si une suite est ω-convergente, sa ω-limite est unique.
- si
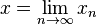
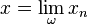
Une caractérisation importante des espaces compacts est que toute suite est ω-convergente (ce résultat est vrai en fait même pour des espaces topologiques quelconques, en généralisant la définition) ; comme on l'a dit, la ω-limite est d'ailleurs nécessairement unique. En particulier, toute suite bornée de nombres réels admet une ω-limite, puisque tout intervalle fermé de

Cônes asymptotiques
Les cônes asymptotiques d'espaces métriques forment une importante classe d'ultralimites. Soit (X,d) un espace métrique, ω un ultrafiltre (non trivial) sur

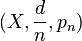
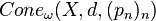
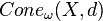
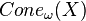
Cette construction joue un rôle important dans la théorie géométrique des groupes, car les cônes asymptotiques (ou plus précisément leurs types topologiques et leurs types lipschitziens) fournissent des invariants quasi-isométriques des espaces métriques en général et des groupes à nombre fini de générateurs en particulier. Les cônes asymptotiques se sont également révélés utiles dans l'étude des groupes relativement hyperboliques et de leurs généralisations.