Variance (statistiques et probabilités) - Définition

Variance d'un vecteur aléatoire

Si l'on définit comme un vecteur aléatoire qui comporte k variables et Μ comme le vecteur des k espérances de X, on définit alors la variance comme:

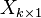
Il s'agit alors d'une matrice carrée de taille k, appelée matrice de variance-covariance, qui comporte sur sa diagonale les variances de chaque composante du vecteur aléatoire et en dehors de la diagonale les covariances. Cette matrice est symétrique et semi-définie positive ; elle est définie positive si et seulement si la seule combinaison linéaire certaine (c'est-à-dire presque sûrement constante) des composantes du vecteur aléatoire est celle dont tous les coefficients sont nuls.

On a les propriétés suivantes: