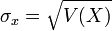Variance (statistiques et probabilités) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistique et probabilité, la variance est une mesure arbitraire servant à caractériser la dispersion d'une distribution ou d'un échantillon.
Définition
Soit X une variable aléatoire réelle dont le moment d'ordre 2, à savoir
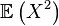
On peut interpréter la variance comme la moyenne des carrés des écarts à la moyenne (rigoureusement: l'espérance des carrés des écarts à l'espérance, vulgairement: Moyenne des carrés moins le carré des moyennes). Elle permet de caractériser la dispersion des valeurs par rapport à la moyenne. Ainsi, une distribution avec une même espérance et une variance plus grande apparaîtra comme plus étalée. Le fait que l'on prenne le carré de ces écarts à la moyenne évite que des écarts positifs et négatifs ne s'annulent.
Notation — On note souvent:
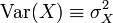
Écart type
L'écart type est la racine carrée de la variance:
Propriétés
- La variance est toujours positive ou nulle.
- Lorsque la variance est nulle, cela signifie que la variable aléatoire correspond à une constante (toutes les réalisations sont identiques).
- Formule alternative de calcul de la variance:
Propriété —
![\operatorname{Var}(X)=\mathbb{E}\left[X^2\right]-\mathbb{E}[X]^2](https://static.techno-science.net/illustration/Definitions/autres/4/418072716adbd43c6921a70d260af4cf_8e782657e60df8371830151838a5a884.png)
-
- Cette formule s'énonce ainsi : la variance est égale à l'espérance du carré de X moins le carré de l'espérance de X. La formule permet souvent un calcul plus simple de la variance que la définition.
-
- Sa démonstration est faite dans le théorème de König-Huyghens.
- Variance d'une transformation affine:
Propriété —
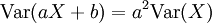
Pour cette démonstration, il est utile de rappeler une des propriétés de l'espérance:
Propriété —
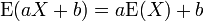
On a alors:
![\begin{align}\operatorname{Var}(aX+b)& = E[(aX+b -E[aX+b])^2] \qquad \text{Selon definition de la variance}\\ & = E[(aX+b -aE[X]-b)^2] \\& = E[(aX -aE[X])^2]\\& = E[a^2(X -E[X])^2]\\& = a^2E[(X -E[X])^2] \\&= a^2\operatorname{Var}(X) \end{align}](https://static.techno-science.net/illustration/Definitions/autres/0/0f93cd34ed8f70e42182f6f512120f00_3f74f16f636b08cbb212e6c28dbf7a45.png)
-
- On remarque à travers cette propriété que le fait de déplacer simplement une distribution (ajouter +b) ne modifie pas sa variance. Par contre, changer l'échelle (multiplier par a) modifie la variance quadratiquement. Cette propriété permet également de confirmer la remarque établie précédemment que la variance d'une constante est nulle, en effet,
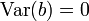
- On remarque à travers cette propriété que le fait de déplacer simplement une distribution (ajouter +b) ne modifie pas sa variance. Par contre, changer l'échelle (multiplier par a) modifie la variance quadratiquement. Cette propriété permet également de confirmer la remarque établie précédemment que la variance d'une constante est nulle, en effet,
- Variance de la somme de deux variables
Si
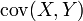
Propriété —
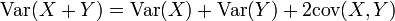
- Variance de la somme de deux variables indépendantes (et plus généralement non corrélées)
Propriété —
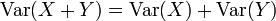
-
- Il faut faire attention au fait que
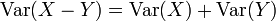
- Il faut faire attention au fait que
- Bilinéarité
Propriété —
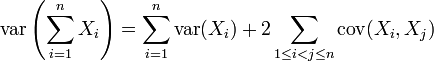
-
- Cette formule est classique pour une forme quadratique associée à une forme bilinéaire symétrique. Dans ce cas particulier, cela traduit le fait que la covariance est une forme bilinéaire symétrique positive (sur l'espace vectoriel
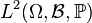
- Cette formule est classique pour une forme quadratique associée à une forme bilinéaire symétrique. Dans ce cas particulier, cela traduit le fait que la covariance est une forme bilinéaire symétrique positive (sur l'espace vectoriel
Propriété —
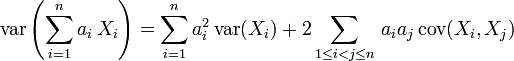
- Variance de la moyenne de variables indépendantes (ou 2 à 2 non corrélées) et de même variance σ2
En définissant
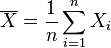
Propriété —
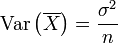
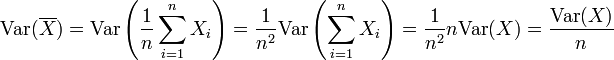
![\operatorname{Var}(X)\equiv V(X) \equiv \mathbb{E}\left[(X-\mathbb{E}[X])^2\right]](https://static.techno-science.net/illustration/Definitions/autres/b/b087ddd44e892c759103657e5d42b810_d243bddab4949f4ad7874721ac6f716c.png)