Variété algébrique affine - Définition

Définition formelle

Une variété (algébrique) affine sur un corps k est un espace localement annelé de la forme (X,O_X) où X est le spectre maximal d'une k-algèbre de type fini A muni de la topologie de Zariski, et où O_X est le faisceau des fonctions régulières sur X. S'il n'y a pas de confusion possible, la variété affine (X,O_X) sera notée simplement X.

Un morphisme de variétés affines est un morphisme d'espaces localement annelés .

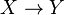
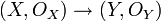
Exemple La variété affine s'appelle l'espace affine de dimension n sur k.

Espaces tangent et cotangent de Zariski

Puisque les polynômes se dérivent formellement (et que leurs dérivées sont des polynômes), on peut algébriser une partie des calculs de la géométrie différentielle. Il est notamment possible d'effectuer des calculs linéaires sur une variété algébrique Spm A en chacun de ses points m, en y construisant un espace vectoriel tangent et cotangent. Ces espaces vectoriels s'obtiennent à partir de l'anneau localisé A_m.