Variété algébrique affine - Définition
La liste des auteurs de cet article est disponible ici.
Faisceau des fonctions régulières
Lorsque k est algébriquement clos et A est réduit, tout élément f de A peut s'identifier à une application
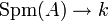
![A=k[X_1,\ldots, X_n]](https://static.techno-science.net/illustration/Definitions/autres/2/25fc3735be403f1f3b1b94771064f49c_633dfeed5a8e7edae298747e1dc79cb7.png)
Par analogie, dans le cas général (k quelconque, et A non nécessairement réduit), les éléments de A sont appelés des fonctions régulières sur Spm(A) (par opposition aux fonctions rationnelles qui peuvent avoir des pôles). Et puisque la localisation Af a pour spectre maximal D(f), il est naturel d'appeler les éléments de Af des fonctions régulières sur l'ouvert D(f).
Pour définition les fonctions régulières sur des ouverts quelconques de Spm(A), nous avons besoin de la notion de faisceaux sur Spm(A).
Proposition: Soit X l'espace topologique Spm(A). À isomorphisme près, il existe un unique faisceau d'anneaux commutatifs OX sur X dont l'anneau des sections sur tout ouvert principal D(f) s'identifie à l'anneau localisé Af. Pour tout idéal maximal m de A, l'anneau des germes de fonctions régulières en m (vu comme un point de X) s'identifie au localisé Am de A en m.
Pour tout ouvert U, les éléments de OX(U) sont appelés des fonctions régulières sur U. Le couple X,OX est un espace localement annelé. Et le faisceau OX est appelé le faisceau structural de (X,OX).
Exemples
- Si
![X={\rm Spm}(k[X_1,\ldots, X_n])](https://static.techno-science.net/illustration/Definitions/autres/a/a3c62a36c72fab9a59f619ef2c42e344_642de1dd7b8add7d853882157a155017.png)
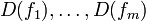
![O_X(U)=k[X_1, \ldots, X_n]_f](https://static.techno-science.net/illustration/Definitions/autres/c/c9e1b3f2a78d54dc5198dd0c2c9fdd5a_6d6a77c74e514702072535a145635888.png)
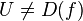
- Supposons A intègre de corps des fractions K. Alors toute localisation de A se plonge canoniquement dans K. Les fonctions régulières sur un ouvert U sont alors les fractions α telle que pour tout ouvert principal D(f) contenu dans U, α peut s'écrire sous la forme g / fn pour un
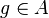
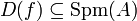
Si
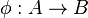
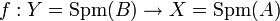
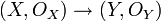
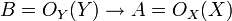
Dimension de Krull
On définit désormais une variété algébrique affine comme Spm A, avec A une K-algèbre de type fini. Une variété affine est alors naturellement munie de la topologie de Zariski. Ici nous ne considérons que le spectre maximal et non la totalité du spectre premier, il n'y a donc pas de points génériques et les variétés affines vérifient l'axiome de séparation T1, au lieu de T0.
Avec la topologie de Zariski on a une bonne définition de la dimension, la dimension de Krull, qui coïncide avec l'intuition sur les cas simples.
Premières propriétés
- Un morphisme de variétés affines
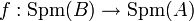
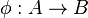
![{\rm Spm} (k[X_1,\ldots, X_n]/I)\to {\rm Spm}(k[Y_1,\ldots, Y_m]/J)](https://static.techno-science.net/illustration/Definitions/autres/5/590cfd75d1abce8bd6ef582746342e7d_1b7f9eb5fd4ca100698f6030b3c2037f.png)
est toujours donné par un morphisme de k-algèbres
![\psi : k[Y_1,\ldots, Y_m]\to k[X_1, \ldots, X_n]](https://static.techno-science.net/illustration/Definitions/autres/8/842331c5f7ce33ba5d685af3a2945395_32b5b96684cdf2169b3aa0429568d502.png)
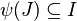
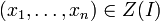
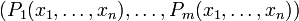
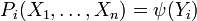
- Toute sous-variété fermée d'une variété affine Spm(A) est une variété affine Spm(A / I) pour un idéal I.
- Pour tout
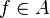
- En général, il existe des sous-variétés ouvertes affines de Spm(A) qui ne sont pas de la forme Spm(Af), et il existe des sous-variétés ouvertes qui ne sont pas affines.

















































