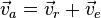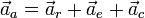Composition des mouvements - Définition
La loi de composition des mouvements permet en mécanique newtonienne de relier les accélérations et les vitesses observées dans deux référentiels distincts. C'est une loi de cinématique c'est-à-dire essentiellement de description. Néanmoins, elle permet d'introduire le concept de forces d'inertie dans un référentiel non galiléen.
Cadre
Soit (R) et (R') des référentiels respectivement centrés en O et A, et
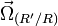
La loi de composition des mouvements se démontre grâce à la propriété suivante: si
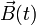
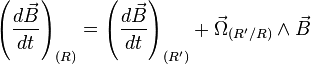
|
Composition des vitesses
Soit M un point mobile dans l'espace. On définit:
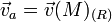
- La vitesse relative de M est la vitesse de M dans (R') notée :
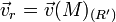
- La vitesse d'entraînement est la vitesse de M par rapport à (R) si il était fixe dans (R') notée :
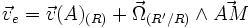
La loi de composition est assez intuitive puisqu'elle s'écrit:
|
|
Composition des accélérations
La composition des accélérations est beaucoup moins intuitive, car elle fait intervenir non seulement une accélération d'entraînement, mais aussi une accélération complémentaire dite de Coriolis, qui n'a été découverte qu'au XIXe siècle par Gaspard-Gustave Coriolis. On définit ainsi:
- L'accélération absolue de M comme l'accélération de M dans (R), notée :
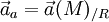
- L'accélération relative de M comme l'accélération de M dans (R'), notée :
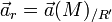
- L'accélération d'entraînement comme l'accélération de M dans (R) s' il était fixe dans (R') :
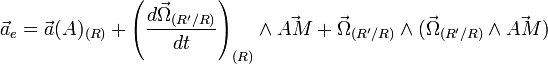
- L' accélération de Coriolis:
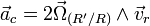
La formule de composition des accélérations est alors donnée par:
|
|