Chirp - Définition

Un chirp (mot d'origine anglaise signifiant " gazouillis ") est par définition^[1] un signal pseudo-périodique c modulé en fréquence autour d'une fréquence porteuse et également modulée en amplitude par une enveloppe a dont les variations sont lentes par rapport aux oscillations de la phase φ:

La partie réelle de ce signal est tout simplement:

Cas particulier du chirp linéaire

On considère souvent le cas particulier du chirp à rampe de fréquence linéaire et à enveloppe constante A qui est tellement courant d'utilisation que l'on a tendance à ramener la notion de chirp à ce seul cas particulier:

Dans les applications radar ou sonar le chirp linéaire est souvent le signal utilisé pour réaliser la compression d'impulsion. L'impulsion étant de durée finie, l'amplitude est une fonction porte. Si le signal est de durée T, débute à t = 0 et balaie la bande de fréquence Δf centrée sur f₀, ce signal s'écrit:

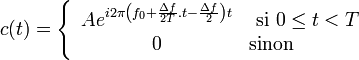
(mais il n'est pas interdit d'utiliser un signal différent)

On montre^[2] que si alors l'amplitude du spectre du chirp linéaire est bien approximée par:

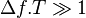
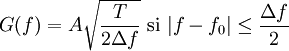
et presque 0 ailleurs.

Exemple de chirp

Exemple acoustique:  ^{Chirp linéaire (5 répétitions)}

Le chirp dans la nature

Le chirp dans sa forme la plus générale donne une bonne modélisation du chant des oiseaux (d'où le nom anglais), des vocalises de cétacés. Les signaux émis par les dauphins et les chauve-souris pour réaliser de l'écho-localisation sont également des chirps, mais beaucoup plus complexes que ceux utilisés par l'Homme en sonar et en radar.

Application en radar et sonar

Voir l'article Compression d'impulsion. La notion de chirp revient également dans le cadre du radar ou sonar à antenne synthétique.

Application en neuroscience

Le chirp peut être utilisé pour tester les propriétés de résonance d'un système. L'avantage principal étant que l'on peut voir approximativement la fréquence de résonance du système avant même d'analyser la réponse au signal par une transformée de Fourier.

En particulier, certains neurones ont une fréquence intrinsèque entre 4 et 8Hz.

Lecture suggérée:

• Hutcheon B et Yarom Y, "Resonance, oscillation and the intrinsic frequency preferences of neurons" ; Trends Neurosci. 2000 May;23(5):216-22.

Terminologie francophone

Le praticien radar ou sonar utilisera volontiers le terme de chirp même en français, et des néologismes tels que le verbe chirper sont fréquemment entendus dans le milieu. Etant donné que le chirp usuel n'est qu'une impulsion modulée en rampe de fréquence, cette dernière expression est également utilisée. Il ne faut pas confondre, par contre, chirp et compression d'impulsion (en anglais: pulse compression) dans la mesure où le premier terme est l'outil et le second une application.

Chirp

Le chirp est aussi une technique de scratch utilisé par les dj qui se décompose en 6 mouvements.