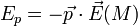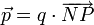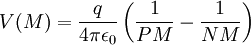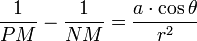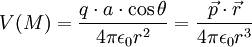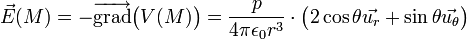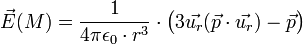Dipôle électrostatique - Définition

Un dipôle électrostatique se définit par un couple de 2 points P et N de charge respective +q et -q distants de a.

Cette notion est principalement utilisée en chimie où certaines liaisons entre molécules peuvent être expliquées en modélisant ces molécules par un dipôle (liaison hydrogène par exemple).

En physique, on s'intéresse au champ électrique crée en un point M éloigné du dipôle (on parle alors de dipôle actif). Mais on peut aussi étudier le comportement du dipôle lorsqu'il est placé dans un champ extérieur (on parle alors de dipôle passif).

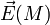
Moment dipolaire

Nous allons définir une grandeur qui caractérise un dipôle électrostatique: son moment dipolaire donné par:

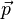
(On rappelle que le point P a la charge +q, le point N la charge -q.)

Le moment dipolaire est exprimé en Coulomb-mètre (Cm) ; par mesure de commodité, on l'exprimera en Debye (D) :

1 D = 3,33564 × 10^-30 Cm

Dipôle actif

Potentiel généré

Le potentiel V(M) crée par le dipôle en M est donné d'après la loi de Coulomb par :

On suppose en outre que le point M est très éloigné du dipôle.

Si l'on se place en coordonnées polaires avec pour origine O milieu de [PN] et pour axe polaire la droite (PM) (cf. schéma à droite), cette hypothèse se traduit par , et on a alors par un développement limité :

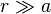
On obtient alors la formule suivante :

Les équipotentielles loin du dipôle sont alors données par l'équation (cf. graphique à droite).

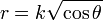
Champ électrique généré

La connaissance de V(M) nous permet de déduire directement par la formule :

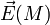
D'où la formule :

On en déduit les lignes de champ (orthogonales aux équipotentielles) loin du dipôle : r = ksin²θ (cf. graphique à droite).

Dipôle passif

Soit un dipôle de moment dipolaire placé en M où règne un champ extérieur .

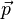
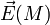
On montre alors que le dipôle subit une force électrostatique dont l'expression est donnée par:

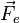
Il subit aussi un moment donné par:

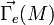
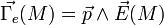
Enfin, dans le cas où l'axe du dipôle ne peut pas tourner, on peut lui associer une énergie potentielle électrique