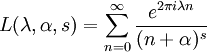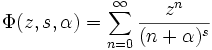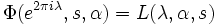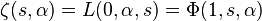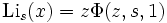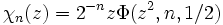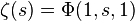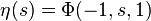Fonction zeta de Lerch - Définition
En mathématiques, la fonction zeta de Lerch est une fonction spéciale qui généralise la fonction zeta d'Hurwitz et le polylogarithme. Elle est donnée par
La fonction zeta de Lerch est reliée à la fonction transcendante de Lerch, qui est donnée par
par
Cas particuliers
La fonction zeta d'Hurwitz est un cas particulier, donnée par
Le polylogarithme est un cas particulier de la fonction zeta de Lerch, donné par
La fonction chi de Legendre est un cas particulier, donnée par
La fonction zeta de Riemann est le cas particulier suivant :
Enfin, la fonction eta de Dirichlet admet l'expression