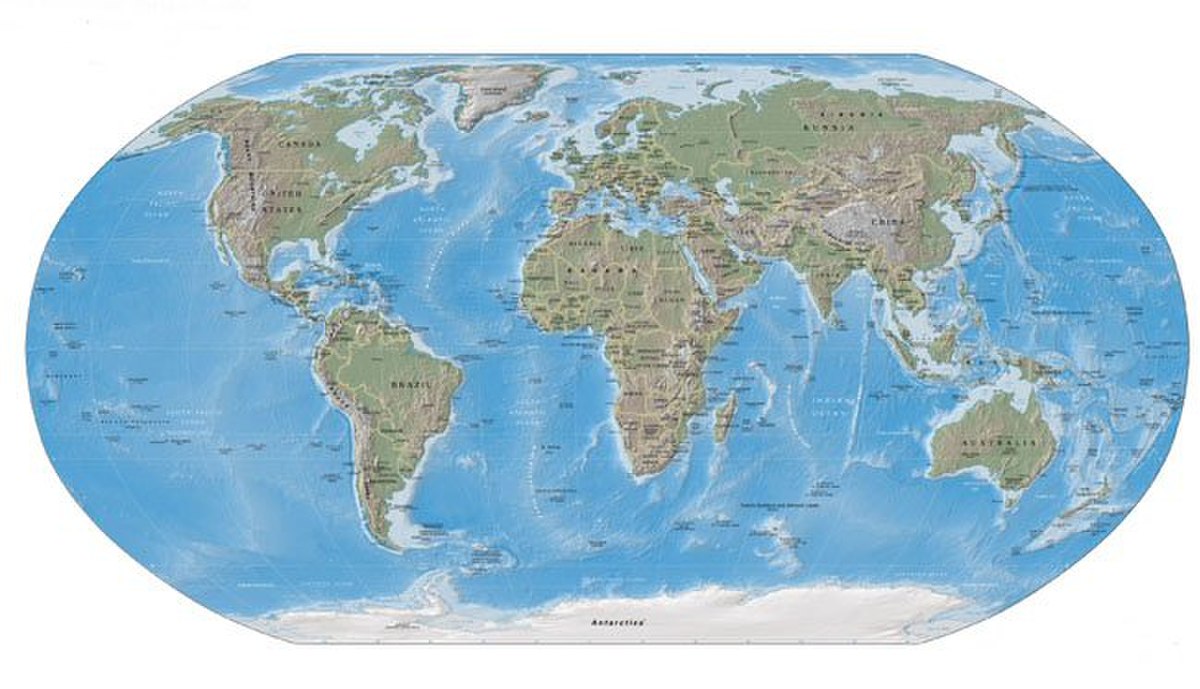
Projection de Robinson - Définition

Projection de Robinson

La projection de Robinson est une projection cartographique utilisée pour les cartes du monde.

Cette projection a été présentée en 1963 par Arthur H. Robinson. La définition de cette projection n'est pas mathématique mais est définie selon Robinson par une série de coordonnées cartésiennes pour un grand nombre de points, et par interpolation pour les autres.

Cette projection est définie comme pseudo-cylindrique car les parallèles sont des segments et les méridiens sont espacés régulièrement.

Dans cette projection on retrouve :

• les lignes de latitude constante sont des parallèles
• les parallèles sont régulièrement espacées entre 38°S et 38°N puis l'écart entre deux parallèles diminue
• un méridien central droit
• les méridiens sont courbes et espacés régulièrement
• les pôles sont représentés par des segments qui font 0,5322 fois la taille de l'équateur