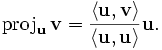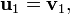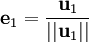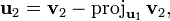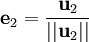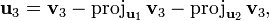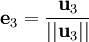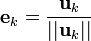Jeudi 18 Avril 2024
Mathématiques

Procédé de Gram-Schmidt - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En algèbre linéaire, le procédé de Gram-Schmidt est une méthode pour orthonormaliser une famille libre de vecteurs d'un espace vectoriel muni d'un produit scalaire.

À partir d'une famille libre (v_1,...,v_n) \,, on construit une famille orthonormale (e_1,...,e_n) \, qui engendre les mêmes espaces vectoriels successifs :

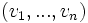
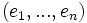
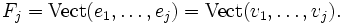
pour tout j inférieur à n, F_j=\mathrm{Vect}(e_1, \dots, e_j)=\mathrm{Vect}(v_1, \dots, v_j).

L'étape générale de l'algorithme consiste à soustraire au vecteur vj + 1 sa projection orthogonale sur l'espace Fj. On s'appuie sur la famille orthonormale déjà construite pour le calcul de projection.

Le procédé peut également être appliqué à une famille libre de vecteurs indexée par \mathbb{N}.

Cette méthode a été nommée en hommage à Jørgen Pedersen Gram et Erhard Schmidt, mais elle est plus ancienne, et est retrouvée dans des travaux de Laplace et Cauchy.

Procédé de Gram-Schmidt

Nous définissons l'opérateur de projection sur une droite vectorielle par :

\mathrm{proj}_{\mathbf{u}}\,\mathbf{v} = {\langle \mathbf{u}, \mathbf{v}\rangle\over\langle \mathbf{u}, \mathbf{u}\rangle}\mathbf{u}.

Le procédé de Gram-Schmidt est alors :

\mathbf{u}_1 = \mathbf{v}_1, \mathbf{e}_1 = {\mathbf{u}_1 \over ||\mathbf{u}_1||}
\mathbf{u}_2 = \mathbf{v}_2-\mathrm{proj}_{\mathbf{u}_1}\,\mathbf{v}_2, \mathbf{e}_2 = {\mathbf{u}_2 \over ||\mathbf{u}_2||}
\mathbf{u}_3 = \mathbf{v}_3-\mathrm{proj}_{\mathbf{u}_1}\,\mathbf{v}_3-\mathrm{proj}_{\mathbf{u}_2}\,\mathbf{v}_3, \mathbf{e}_3 = {\mathbf{u}_3 \over ||\mathbf{u}_3||}
\vdots \vdots
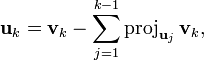
\mathbf{u}_k = \mathbf{v}_k-\sum_{j=1}^{k-1}\mathrm{proj}_{\mathbf{u}_j}\,\mathbf{v}_k, \mathbf{e}_k = {\mathbf{u}_k\over||\mathbf{u}_k||}
D'où vient cette structure fractale observée dans une bactérie ?
Il y a 8 heures
Découverte majeure dans les allergies respiratoires
Il y a 8 heures
Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers
Il y a 13 heures
Propagation inquiétante de la "mouche noire" suceuse de sang en Allemagne
Il y a 13 heures
Le hasard confère le prix Turing et 1 million de dollars au mathématicien Avi Wigderson
Il y a 15 heures
AI Act: comment encadrer l'intelligence artificielle en Europe ?
Il y a 15 heures
Quelle est cette forme étrange photographiée près de la Lune ?
Il y a 1 jour
Si vous avez déjà eu une entorse de la cheville, attention à ceci
Il y a 1 jour
Démonstration d'une nouvelle technologie de lévitation, stable et sans supraconductivité
Il y a 1 jour
Ces indices d'une rupture imminente de la faille de San Andreas
Il y a 1 jour
Cet effet inattendu de la musculation sur la mémoire
Il y a 1 jour
Les géantes Uranus et Neptune ne seraient pas faites comme nous l'imaginions
Il y a 1 jour
Parker Solar Probe se prépare à battre le record de vitesse de l'humanité
Il y a 2 jours
Nos ancêtres à l'époque des dinosaures
Il y a 2 jours
Observer directement le Big Bang avec un télescope plus puissant que le James Webb ?
Il y a 2 jours
Découverte de 17 variants génétiques liés à la maladie d'Alzheimer
Il y a 2 jours
Un immense glacier du Groenland est littéralement en train de fondre sous nos yeux
Il y a 2 jours
Découverte: des bactéries anticholestérol dans notre intestin
Il y a 2 jours
Des dinosaures aux oiseaux: cette anomalie de l'ADN a trompé les scientifiques
Il y a 3 jours
De la vie cachée 800 mètres sous terre: comment est-ce possible ?
Il y a 3 jours
Analyse d'un signal radio inhabituel, en provenance de cet objet spatial extrême
Il y a 3 jours
Ce liquide est programmable, pouvant changer de consistance et de couleur
Il y a 3 jours
Un trou noir trop léger, ou une étoile à neutrons trop lourde ? L'objet qui intrigue les scientifiques
Il y a 3 jours
Un lien démontré entre vapotage, petit-déjeuner et maux de tête
Il y a 3 jours
Un immense "arc-en-ciel" détecté sur une exoplanète
Il y a 4 jours
Des scientifiques étudient 40 ans de vie marine dans... des conserves de saumon
Il y a 4 jours
Cette innovation va améliorer significativement la sensibilité des détecteurs d'ondes gravitationnelles
Il y a 4 jours
Découverte d'une ingénierie humaine vieille de... 300 000 ans
Il y a 4 jours
Psyche: une mission à la découverte de ce très mystérieux objet spatial
Il y a 5 jours
Peur généralisée: des scientifiques découvrent comment ne pas être tétanisé par la peur
Il y a 5 jours
Découverte accidentelle d'une mémoire quantique au potentiel énorme
Il y a 5 jours
Des chercheurs ont créé artificiellement des "minifoies"
Il y a 5 jours
Surprise: la surface lunaire a "coulé" sous la croûte
Il y a 6 jours
Un curieux "point de bascule" découvert dans l'évolution des champignons
Il y a 6 jours
Des humains préhistoriques ont gravé ces traces de dinosaures
Il y a 6 jours
Ralentissement significatif d'importants courants océaniques: des répercussions graves ?
Il y a 6 jours
Les étoiles à neutrons, des aspirateurs de matière noire ?
Il y a 6 jours
Greffer de la peau de porc pour soigner les plaies
Il y a 6 jours
Le secret d'une jeunesse éternelle à proximité du trou noir de notre Voie Lactée
Il y a 7 jours
Une quantité phénoménale de volcans cachés sous l'Antarctique: des risques d'éruption ?
Il y a 7 jours
Une mission spatiale dans l'espace interstellaire, à 1000 unités astronomiques ?
Il y a 7 jours
Ce régime montre une efficacité contre la maladie d'Alzheimer
Il y a 7 jours
Les dinosaures contredisent ce principe scientifique
Il y a 7 jours
Sentons-nous le goût des aliments uniquement avec notre langue ?
Il y a 7 jours
Nova: une rare et impressionnante explosion stellaire bientôt visible dans le ciel
Il y a 8 jours
Découverte d'une importante vertu anti-vieillissement à cette vitamine
Il y a 8 jours
Quand le cerveau ne perçoit que des visages distordus: la prosopométamorphopsie
Il y a 8 jours
La future station lunaire Gateway sous le feu des radiations spatiales
Il y a 8 jours
Cette découverte pourrait améliorer considérablement l'efficacité des traitements contre le cancer
Il y a 8 jours
Les orages violents en France sont déjà intensifiés par le changement climatique
Il y a 8 jours
Populaires
Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers
Parker Solar Probe se prépare à battre le record de vitesse de l'humanité
Ces indices d'une rupture imminente de la faille de San Andreas
De la vie cachée 800 mètres sous terre: comment est-ce possible ?
Découverte majeure dans les allergies respiratoires
D'où vient cette structure fractale observée dans une bactérie ?
Toutes les ventes flash et Codes Promos Amazon
Cdiscount: les meilleures réductions actuelles
Page générée en 0.005 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise