Méthode de Jacobi - Définition

La méthode de Jacobi, due au mathématicien allemand Karl Jacobi, est une méthode iterative de résolution d'un système matriciel de la forme Ax=b. Pour cela, on utilise une suite x^(k) qui converge vers un point fixe x, solution du système d'équations linéaires.

Principe de construction

On cherche à construire l'algorithme pour x⁽⁰⁾ donné, la suite x^{(k + 1)} = F(x^(k)) avec .

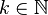
A = M − N où M est une matrice inversible.
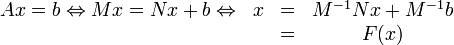
où F est une fonction affine.

Algorithme

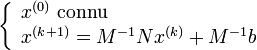
Si x est solution de Ax = b alors x = M ^{− 1}Nx + M ^{− 1}b .

Vecteur erreur

Soit e^(k) le vecteur erreur

e^{(k + 1)} = x^{(k + 1)} − x^(k) = M ^{− 1}N(x^(k) − x^{(k − 1)}) = M ^{− 1}Ne^(k)
On pose B = M ^{− 1}N, ce qui donne e^{(k + 1)} = Be^(k) = B^{(k + 1)}e⁽⁰⁾.

Convergence

L'algorithme converge si (matrice nulle).

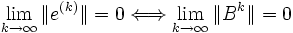
Théorème : Une condition nécessaire et suffisante pour que est que le rayon spectral (plus grande valeur propre en module) de B soit strictement inférieur à 1.
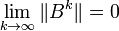
Théorème : La méthode converge quel que soit x⁽⁰⁾ pour les systèmes linéaires dont la matrice est à diagonale strictement dominante.

Méthode de Jacobi

On décompose la matrice A de la façon suivante : A = D-E-F avec D la diagonale, -E la partie en dessous de la diagonale et -F la partie au dessus. Dans la méthode de Jacobi, on choisit M = D et N = E+F (dans la méthode de Gauss-Seidel, M = D-E et N = F).

x^{(k + 1)} = D ^{− 1}(E + F)x^(k) + D ^{− 1}b avec
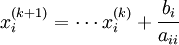
pour la ligne i de D ^{− 1}(E + F) :

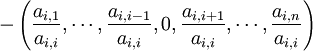
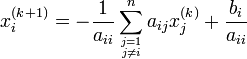
Vecteur résidu

Soit r^(k) = De^(k) le vecteur résidu. On peut écrire avec que l'on calcule de la manière suivante : .

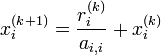
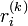
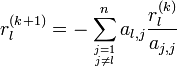
Test d'arrêt

Pour le test d'arrêt, on utilise le vecteur résidu, ce qui donne, pour une précision donnée ε :

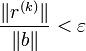
Conclusion

Cette méthode a un coût de l'ordre de 3n²+2n par itération, elle est très facilement parallélisable contrairement à la méthode de Gauss-Seidel, mais qui converge plus vite.