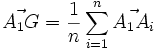Calcul du centre de gravité d'un polygone - Définition
Soit
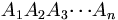
Il s'agit d'un cas particulier de barycentre.
Le centre de gravité d'un triangle se situe au point de concours des médianes. Il se trouve aux 2/3 de la longueur de chaque médiane, plus loin du sommet que du milieu du bord opposé.
Le centre de gravité d'un parallélogramme est le milieu des diagonales.
Polygone régulier
Si le polygone est régulier, son centre de gravité est également centre des cercles inscrit et circonscrit au polygone. Dans le cas où le polygone a un nombre pair de côtés, le centre de gravité est au milieu des segments joignant un côté au côté opposé ; il est centre de symétrie pour le polygone.